
【题目】计算下列各题
(1)计算: ![]() ﹣(
﹣( ![]() )﹣1+(π﹣
)﹣1+(π﹣ ![]() )0﹣(﹣1)100;
)0﹣(﹣1)100;
(2)已知|a+1|+(b﹣3)2=0,求代数式( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() 的值.
的值.
【答案】
(1)解:原式=3﹣4+1﹣1=﹣1
(2)解:∵|a+1|+(b﹣3)2=0,
∴a+1=0,b﹣3=0,即a=﹣1,b=3.
则原式= ![]() ÷
÷ ![]() =
= ![]() ×
× ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]()
【解析】(1)原式第一项利用二次根式的化简公式计算,第二项利用负指数幂法则计算,第三项利用零指数幂法则计算,最后一项利用乘方的意义化简,计算即可得到结果;(2)利用非负数的性质求出a与b的值,原式通分并利用同分母分式的加法法则计算,将a与b的值代入计算即可求出值.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对整数指数幂的运算性质的理解,了解aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
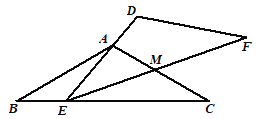
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.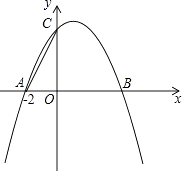
(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,点D在AB的延长线上. 
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法). ①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
(2)由(1)得:BF与边AC的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场促销,小鱼将促销信息告诉了妈妈,假设某一商品的定价为![]() ,并列出不等式为
,并列出不等式为![]() ,那么小鱼告诉妈妈的信息是( )
,那么小鱼告诉妈妈的信息是( )
A. 买两件等值的商品可减100元,再打三折,最后不到1000元
B. 买两件等值的商品可打三折,再减100元,最后不到1000元
C. 买两件等值的商品可减100元,再打七折,最后不到1000元
D. 买两件等值的商品可打七折,再减100元,最后不到1000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,BE平分∠ABC交AC边于点E,过点E作DE∥BC交AB于点D,
(1)求证:△BDE为等腰三角形;
(2)若点D为AB中点,AB=6,求线段BC的长;
(3)在图2条件下,若∠BAC=60°,动点P从点B出发,以每秒1个单位的速度沿射线BE运动,请直接写出图3当△ABP为等腰三角形时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,∠BAC=30°,点 D 是 BC 边上的点,AB=18,将△ABC 沿直线 AD 翻折,使点 C 落在 AB 边上的点 E 处,若点 P 是直线 AD 上的动点,则 BP+EP 的最小值是____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com