
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
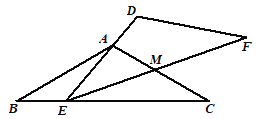
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
【答案】(1)证明见解析;(2)见解析;(3)见解析.
【解析】
(1)已知△ABC≌△DEF,根据全等三角形的性质可得∠ABC=∠DEF,又因∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC,即可得∠B+∠BAE=∠AEM+∠MEC,所以∠BAE=∠MEC;(2)当E为BC中点时, AB=AC,根据等腰三角形三线合一的性质可得AE⊥BC,∠EAM=60°,再由∠DEM=30°即可证得AC⊥EF; 在Rt△ABE中,∠B=30°,![]() ,求得BE=
,求得BE=![]() ,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=
,即可求得BC=3;在Rt△CEM中,∠C=30°,EC=![]() E,求得EM=
E,求得EM=![]() ,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=
,根据全等三角形的性质可得BC=EF=3,所以FM= EF-EM=![]() ,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、
,即可得EM:FM=1:3 ;(3)分AM=AE、EA=EM、![]() 三种情况求解即可.
三种情况求解即可.
(1)证明:∵△ABC≌△DEF
∴∠ABC=∠DEF
∵∠AEC=∠B+∠BAE,∠AEC=∠AEM+∠MEC;
∴∠B+∠BAE=∠AEM+∠MEC,
即∠BAE=∠MEC ;
(2)当E为BC中点时,
∵AB=AC,
∴AE⊥BC,BE=EC=![]() ,∠EAM=60°,
,∠EAM=60°,
又∵∠DEM=30°,
∴AC⊥EF;
∵![]() ,
,![]() ,
,
∴∠B=∠C=30°,
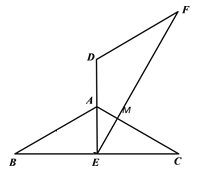
在Rt△ABE中,∠B=30°,![]() ,
,
∴BE=![]() ,
,
∴BC=3;
在Rt△CEM中,∠C=30°,EC=![]() ,
,
∴EM=![]() ,
,
∵△ABC≌△DEF,
∴BC=EF=3,
∴FM= EF-EM=![]() ,
,
∴EM:FM=1:3;
(3)当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.
①当![]() 时,如图,
时,如图,

![]()
![]() ,
,
此时点E与点B重合,与题意矛盾(舍去 ) ;
②当![]() 时,如图,
时,如图,
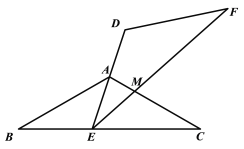
由(1)知,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
③当![]() 时,如图,
时,如图,
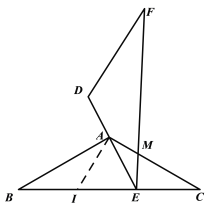
则![]() ,
,
![]() ,
,
取BE中点I,连结AI,
则![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
设![]() ,在
,在![]() 中,
中,
由勾股定理,得![]() ,
,
即![]() ,解得
,解得![]()
![]() .
.
综上所述,当![]() 或2时,
或2时,![]() 是等腰三角形.
是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,SABCD=24,AE平分∠BAC,交BC于E,沿AE将△ABE折叠,点B的对应点为F,连接EF并延长交AD于G,EG将ABCD分为面积相等的两部分.则S△ABE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作∠B的角平分线;
(2)作BC的中垂线;
(3)以BC边所在直线为对称轴,作△ABC的轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上. 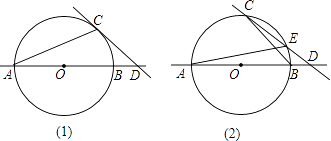
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E.BD:DE:EC=2:3:5,求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现C,D,E在三点中,其中一点是另外两点连线的中点的情形,问这样的情况出现几次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,E,F分别在边AC、BC上,满足AE=CF,连接BE,AF交于点P.
(1)求证:△ABE≌△CAF;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com