
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】
(1)
解:过点C作CD垂直AB延长线于点D,
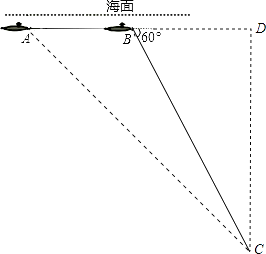
设CD=x米,
在Rt△ACD中,
∵∠DAC=45°,
∴AD=x,
在Rt△BCD中,
∵∠CBD=60°,
∴BD= ![]() x,
x,
∴AB=AD﹣BD=x﹣ ![]() x=2000,
x=2000,
解得:x≈4732,
∴船C距离海平面为4732+1800=6532米<7062.68米,
∴沉船C在“蛟龙”号深潜极限范围内
(2)
解:t=1800÷2000=0.9(小时).
答:“蛟龙”号从B处上浮回到海面的时间为0.9小时
【解析】(1)过点C作CD垂直AB延长线于点D,设CD为x米,在Rt△ACD和Rt△BCD中,分别表示出AD和BD的长度,然后根据AB=2000米,求出x的值,求出点C距离海面的距离,判断是否在极限范围内;(2)根据时间=路程÷速度,求出时间即可.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)计算:( ![]() ﹣2)0+(﹣1)2014+
﹣2)0+(﹣1)2014+ ![]() ﹣sin45°;
﹣sin45°;
(2)先化简,再求值:(a2b+ab)÷ ![]() ,其中a=
,其中a= ![]() +1,b=
+1,b= ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 是两个全等的三角形,
是两个全等的三角形,![]() ,
,![]() .现将
.现将![]() 和
和![]() 按如图所示的方式叠放在一起,
按如图所示的方式叠放在一起,![]() 保持不动,
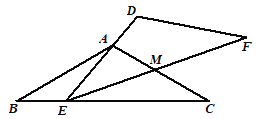
保持不动,![]() 运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
运动,且满足:点E在边BC上运动(不与点B,C重合),且边DE始终经过点A,EF与AC交于点M .
(1)求证:∠BAE=∠MEC;
(2)当E在BC中点时,请求出ME:MF的值;
(3)在![]() 的运动过程中,
的运动过程中,![]() 能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
能否构成等腰三角形?若能,请直接写出所有符合条件的BE的长;若不能,则请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.
(1)根据题意,画出图形,并标上正确的字母;
(2)求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,之间的距离为2 ,
,之间的距离为2 , ![]() ,
,![]() 之间的距离为3 ,则AC2= _______.
之间的距离为3 ,则AC2= _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.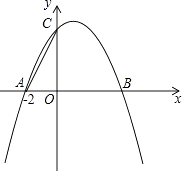
(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,点D在AB的延长线上. 
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法). ①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
(2)由(1)得:BF与边AC的位置关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com