
【题目】在ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.
(1)根据题意,画出图形,并标上正确的字母;
(2)求证:DE=BF.
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=AC,∠BAC=90
中,AB=AC,∠BAC=90![]() ,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE =∠CPF;(3)△EPF是等腰直角三角形;(4)
,直角∠EPF的顶点是BC的中点,两边PE,PF分别交AB,AC于点E,F.给出以下五个结论:(1)AE=CF;(2)∠APE =∠CPF;(3)△EPF是等腰直角三角形;(4)![]() =
=![]()
![]() (5)EF=AP其中一定成立的有________个.
(5)EF=AP其中一定成立的有________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作∠B的角平分线;
(2)作BC的中垂线;
(3)以BC边所在直线为对称轴,作△ABC的轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,E,F分别在边AC、BC上,满足AE=CF,连接BE,AF交于点P.
(1)求证:△ABE≌△CAF;
(2)求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
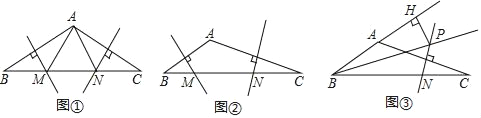
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.
(1)根据题意,画出图形,并标上正确的字母;
(2)求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.

(1)求证:∠BDC=![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com