Question

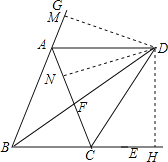
【题目】如图，BD和CD分别平分△ABC的内角∠EBA和外角∠ECA，BD交AC于F，连接AD．

（1）求证：∠BDC=∠BAC；

（2）若AB=AC，请判断△ABD的形状，并证明你的结论；

（3）在（2）的条件下，若AF=BF，求∠EBA的大小．

Answer 1

【答案】（1）见解析；（2）△ABD为等腰三角形；见解析；（3）∠ABC=72°．

【解析】

试题分析：（1）根据角平分线的定义得到∠BDC+∠ABC=∠ACE，∠BAC+∠ABC=∠ACE，于是得到∠BDC+∠ABC=∠BAC+∠ABC，等量代换即可得到结论；

（2）作DM⊥BG于M，DN⊥AC于N，DH⊥BE于H根据角平分线的性质得到DM=DH，DN=DH，等量代换得到DM=DN，根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°，∠BAC+∠ABC+∠ACB=180°，推出∠GAD+∠CAD=∠ABC+∠ACB，由等腰三角形的性质得到∠ABC=∠ACB，等量代换得到∠GAD=∠ABC，推出AD∥BC，由平行线的性质得到∠ADB=∠DBC，证得∠ABD=∠ADB，即可得到结论；

（3）根据等腰三角形的性质得到∠BAF=∠ABF=∠ABC，根据三角形的内角和即可得到结论．

解：（1）∵BD、CD分别平分∠EBA、∠ECA，BD交AC于F，

∴∠BDC+∠ABC=∠ACE，∠BAC+∠ABC=∠ACE，

∴∠BDC+∠ABC=∠BAC+∠ABC，

∴∠BDC=∠BAC．

（2）△ABD为等腰三角形，证明如下：

作DM⊥BG于M，DN⊥AC于N，DH⊥BE于H

∵BD、CD分别平分∠EBA、∠ECA，

∴DM=DH，DN=DH，

∴DM=DN，

∴AD平分∠CAG，即∠GAD=∠CAD，

∵∠GAD+∠CAD+∠BAC=180°，∠BAC+∠ABC+∠ACB=180°，

∴∠GAD+∠CAD=∠ABC+∠ACB，

∵AB=AC，

∴∠ABC=∠ACB，

∴∠GAD=∠ABC，

∴AD∥BC，

∴∠ADB=∠DBC，

又∵∠ABD=∠DBC，

∴∠ABD=∠ADB，

∴AB=AD，

∴△ABD为等腰三角形；

（3）∵AF=BF，

∴∠BAF=∠ABF=∠ABC，

∵∠BAF+∠ABC+∠ACB=180°，∠ABC=∠ACB，

∴∠ABC=180°，

∴∠ABC=72°．