
����Ŀ����ͼ��һ�κ���y=k1x+b��k1��0���뷴��������y=![]() ��k2��0����x��0����ͼ����A��1��6����B��a��3�����㣬
��k2��0����x��0����ͼ����A��1��6����B��a��3�����㣬
��1���ֱ����һ�κ����뷴���������Ľ���ʽ��
��2��ֱ��д��k1x+b��![]() ��0ʱx��x��0����ȡֵ��Χ��
��0ʱx��x��0����ȡֵ��Χ��
��3����ͼ����������OBCD�У�BC��OD��OB=CD��OD����x���ϣ�����C��CE��OD�ڵ�E��CE�ͷ���������ͼ���ڵ�P��������OBCD�����Ϊ12ʱ�����ж�PC��PE�Ĵ�С��ϵ����˵�����ɣ�

���𰸡�(1) һ�κ�������ʽΪ��y=��3x+9����������������ʽΪ��y=![]() ����2��1��x��2����3��PC=PE������������.
����2��1��x��2����3��PC=PE������������.
��������
�����������1���ɷ���������y=![]() ��k2��0����x��0����ͼ���A��1��6����B��a��3�����㣬���ô���ϵ����������÷����������Ľ���ʽ���B�����꣬Ȼ����y=k1x+b��A��1��6����B��2��3�������ô���ϵ�������һ�κ����Ľ���ʽ��
��k2��0����x��0����ͼ���A��1��6����B��a��3�����㣬���ô���ϵ����������÷����������Ľ���ʽ���B�����꣬Ȼ����y=k1x+b��A��1��6����B��2��3�������ô���ϵ�������һ�κ����Ľ���ʽ��
��2�����ͼ�������k1x+b��![]() ��0ʱx��x��0����ȡֵ��Χ��
��0ʱx��x��0����ȡֵ��Χ��
��3�����ȹ���B��BF��OD�ڵ�F����֤��Rt��OBF��Rt��DCE��HL�������ɵ�OF=DE��Ȼ����C��a��3����������OBCD�����Ϊ12���������a��ֵ���̶�����߶�PC��PE�ij������֤�ý��ۣ�
�����������1����y=![]() ��A��1��6����B��a��3����
��A��1��6����B��a��3����
��6=![]() ��3=
��3=![]() ��
��
��k2=6��a=2��
����������������ʽΪ��y=![]() ��B��2��3����
��B��2��3����
��y=k1x+b��A��1��6����B��2��3����
��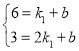 ��
��
��ã�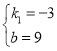 ��
��
��һ�κ�������ʽΪ��y=��3x+9��
��2����ͼ��ã�k1x+b��![]() ��0ʱ��x��x��0����ȡֵ��ΧΪ��1��x��2��
��0ʱ��x��x��0����ȡֵ��ΧΪ��1��x��2��
��3��PC=PE���������£�
����B��BF��OD�ڵ�F��
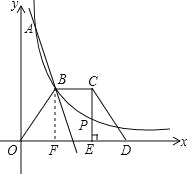
���ı���OBCD�ǵ������Σ�BC��OD��CE��OD��
��OB=CD��BF=CE��
��Rt��OBF��Rt��DCE��
![]() ��
��
��Rt��OBF��Rt��DCE��HL����
��OF=DE��
��B��2��3����
��OF=DE=2��BF=3��
��C��a��3����
��BC=a��2��OD=a+2��
������OBCD�����Ϊ12��
��![]() ��a��2+a+2����3=12��
��a��2+a+2����3=12��
��ã�a=4��
��C��4��3����
��xP=4��
��yP=![]() ��
��
��P��4��![]() ����
����
��C��4��3����E��4��0����
��PC=3��![]() =
=![]() ��
��
PE=![]() ��0=
��0=![]() ��
��
��PC=PE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��DC���ϣ�DE=4��EC=2�����߶�AE�Ƶ�A��ת��ʹ��E����ֱ��BC�ϵĵ�F������FC�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������Ϊ��������״�Ĺ��ţ���ˮ���4��ʱ�����������Ŷ�����ߵ㣩��ˮ��2�ף�ˮ���½�1��ʱ��ˮ��Ŀ���Ϊ �ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AD����ô��������һ�������������ж���ABC�ա�ADC���ǣ�������

A. CB=CD B. ��BAC=��DAC C. ��BCA=��DCA D. ��B=��D=90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij�ֲ�Ʒ�Ľ���Ϊÿ��40Ԫ�����ڵ��ۼ�Ϊÿ��60Ԫ��ÿ���ڿ�����300�����г����鷢�֣��ò�Ʒÿ����1Ԫ��ÿ���ڿɶ�����20�������ڹ�������ԭ���������ó���380���������ֲ�Ʒÿ������xԪ��xΪ��������ÿ���ڵ���������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���ò�Ʒ���ۼ۶�Ϊÿ������Ԫʱ��ÿ���ڵ��������������������Ƕ���Ԫ��
��3���ò�Ʒ���ۼ���ʲô��Χʱ��ÿ���ڵ�����������6000Ԫ����ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����n��������һ��������ÿ��װ��3.5t����ô�����������1.5t�������ߣ����ÿ��װ��4t����ôװ���������ﻹ��һ���ճ�����������������n��ֵΪ(����)
A. 11 B. 9 C. 7 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
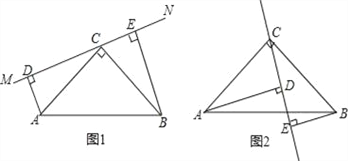
����Ŀ����ͼ��1������ABC�У���ACB=90����AC=BC��ֱ��MN������C����AD��MN�ڵ�D��BE��MN�ڵ�E����֤��
��1����ADC�ա�CEB��
��2��DE=AD+BE��
��3����ֱ��MN�Ƶ�C��ת��ͼ��2����λ��ʱ��DE��AD��BE�������Ĺ�ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�����ҵı����У�����ʽ�ֽ��Ϊ�� ��
A. x2-1=(x+1)(x-1) B. x2-1+y2=(x+1)(x-1) +y2
C. x(a-b)=ax-bx D. ax+bx+c=x(a+b)+c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������һ���ı���ͼ����
��1������ֱ���ABC�Ƶ�O˳ʱ����ת90���ͼ�Σ����ڵ�O�ԳƵ�ͼ���Լ���ʱ����ת90���ͼ�Σ���������Ϳ�ڣ�
��2����������ÿ��С�����εı߳�Ϊ1����ת���A�Ķ�Ӧ������ΪA1��A2��A3�����ı���AA1A2A3�������
��3���������ͼ���ܹ�˵��һ���������۵���ȷ�ԣ���д��������ۣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com