
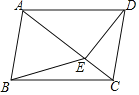
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若△ABE是等边三角形,四边形BCDE的面积等于2![]() ,求CE的长.
,求CE的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用两组对角相等的四边形是平行四边形进行证明;
(2)设CD的长为a,则CE=![]() a,,DE=
a,,DE=![]() a,S△CED=
a,S△CED=![]() a2,由面积关系可得
a2,由面积关系可得![]() a2+
a2+![]() a2=2
a2=2![]() ,可求a的值,即可求CE的长.
,可求a的值,即可求CE的长.
(1)证明:∵AB∥CD,
∴∠DAB+∠ADC=∠ABC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠DAB=∠BCD,且∠ABC=∠ADC,
∴四边形ABCD是平行四边形;
(2)∵△ABE是等边三角形,
∴AB=AE=CD,∠BAC=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°,
∵DE⊥AC,
∴∠DEC=90![]() ,
,
在Rt△CDE中,设CD的长为a,
则CE=![]() a,DE=
a,DE=![]() a,S△CED=
a,S△CED=![]() a2.
a2.
因为△CED与△CEB是同底等高的三角形,
∴S△CED=S△CEB,
又∵S四边形BCDE=S△CED+S△CEB=2![]() ,
,
∴![]() a2+
a2+![]() a2=2
a2=2![]() ,
,
∴a=2![]() ,
,
∴CE=![]() a=
a=![]() .
.


科目:初中数学 来源: 题型:
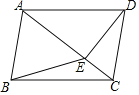
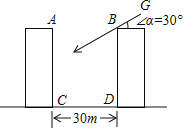
【题目】两栋居民楼之间的距离CD=30米,楼AC和BD均为10层,每层楼高3米.
(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?
(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣4x﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C,点P是抛物线上的一个不与点C重合的一个动点,若S△PAB=S△ABC,则点P的坐标是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,两锐角的度数之比为2:1,其最短边为1,射线CP交AB所在的直线于点P,且∠ACP=30°,则线段CP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
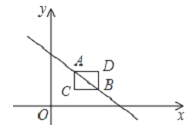
【题目】如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=﹣x+4于B、A两点,若二次函数y=ax2+bx+c的图象经过坐标原点O,且顶点在矩形ADBC内(包括边上),则a的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,AB是⊙O的切线,连接BP并延长,交直线l于点C.
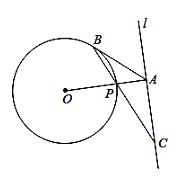
(1)求证AB=AC;
(2)若PC=![]() ,OA=15,求⊙O的半径的长.
,OA=15,求⊙O的半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 、
、![]() 分别与圆相交于
分别与圆相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
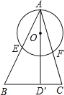
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年10月31日,在广州举行的世界城市日全球主场活动开幕式上,住建部公布许昌成为“国家生态园林城市”在2018年植树节到来之际,许昌某中学购买了甲、乙两种树木用于绿化校园.若购买7棵甲种树和4棵乙种树需510元;购买3棵甲种树和5棵乙种树需350元.
(1)求甲种树和乙种树的单价;
(2)按学校规划,准备购买甲、乙两种树共200棵,且甲种树的数量不少于乙种树的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com