
����Ŀ��2017��10��31�գ��ڹ��ݾ��е����������ȫ���������Ļʽ�ϣ�ס��������������Ϊ��������̬�ֳ�������2018��ֲ���ڵ���֮�ʣ�����ij��ѧ�����˼ס���������ľ�����̻�У��������7�ü�������4����������510Ԫ������3�ü�������5����������350Ԫ��
��1������������������ĵ��ۣ�
��2����ѧУ�滮��������ס�����������200�ã��Ҽ�������������������������������![]() ������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
���𰸡���1���������ĵ���Ϊ50Ԫ/�ã��������ĵ���Ϊ40Ԫ/�ã���2��������67�ü�������133��������ʱ�����������ͣ�
��������
��1����������ĵ���ΪxԪ/�ã��������ĵ���ΪyԪ/�ã�����������7�ü�������4����������510Ԫ������3�ü�������5����������350Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���蹺�������a�ã�������������200-a���ã����ݼ�������������������������������![]() �ɵó�����a��һԪһ�β���ʽ����֮���ɵó�a��ȡֵ��Χ�����ɼ������ĵ��۱��������ĵ��۹����ҳ���ʡǮ�Ĺ�����
�ɵó�����a��һԪһ�β���ʽ����֮���ɵó�a��ȡֵ��Χ�����ɼ������ĵ��۱��������ĵ��۹����ҳ���ʡǮ�Ĺ�����
�⣺��1����������ĵ���ΪxԪ/�ã��������ĵ���ΪyԪ/�ã�
��������ã�![]() ��
��
��ã�![]()
�𣺼������ĵ���Ϊ50Ԫ/�ã��������ĵ���Ϊ40Ԫ/�ã�
��2���蹺�������a�ã�������������200��a���ã�
��������ã�![]()
��ã�![]()
��a������
��a��67��
�������ĵ��۱��������ĵ��۹�
�൱����67�ü�������133��������ʱ�����������ͣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��B��C��ͬһ��ֱ���ϣ���MΪ�߶�AC���е㡢��NΪ�߶�BC���е�.
��1����ͼ������C���߶�AB��ʱ��
�����߶�![]() ����
����![]() �ij��ȣ�
�ij��ȣ�
����AB=a����MN�ij��ȣ�
��2����![]() ����MN�ij��ȣ��ú�
����MN�ij��ȣ��ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У��Խ���AC��BD���ڵ�O����P���߶�BC�ϣ�������B������BPE= ![]() ��ACB��PE��BO�ڵ�E������B��BF��PE������ΪF����AC�ڵ�G��
��ACB��PE��BO�ڵ�E������B��BF��PE������ΪF����AC�ڵ�G��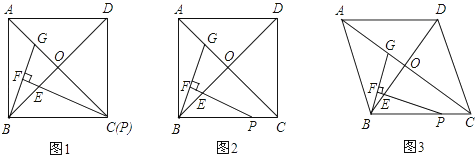
��1������P���C�غ�ʱ����ͼ�٣�����֤����BOG�ա�POE��
��2�����ͼ�ڣ�ͨ���۲졢���������룺 ![]() ��
�� ![]() �Ĺ�ϵ����֤����IJ��룻
�Ĺ�ϵ����֤����IJ��룻
��3����������ABCD��Ϊ���Σ������������䣨��ͼ�ۣ�����AC=8��BD=6��ֱ��д�� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
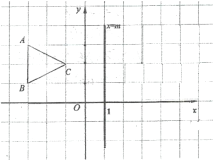
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABC��x=mֱ��.
��1����A(-3,3)��B (-3,1)��C (-1,2)����m=1ʱ����ͼ��������ABC����ֱ��x=m�ԳƵ�ͼ�Σ���ֱ��д��![]() ��
��![]() ��
��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ��
��![]() ��
��![]() �����ꣻ
�����ꣻ
��2�������е�![]() �͵�
�͵�![]() ����ֱ��
����ֱ��![]() �Գƣ���ô
�Գƣ���ô![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ֮����ʲô������ϵ����ֱ��д���𰸼��ɣ�
֮����ʲô������ϵ����ֱ��д���𰸼��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����3��A�ͳ���2��B�ͳ���������һ�ο��˻���19�֣���2��A�ͳ���3��B�ͳ���������һ�ο��˻���21�֣�
��1��1��A�ͳ���1��B�ͳ�����������һ�ηֱ�����˻����ٶ�?
��2��ij������˾����49�ֻ���ƻ�ͬʱ����A�ͳ�![]() ����B�ͳ�
����B�ͳ�![]() ����һ�����꣬��ǡ��ÿ�������������
����һ�����꣬��ǡ��ÿ�������������
����![]() ��
��![]() ��ֵ��
��ֵ��
����A�ͳ�ÿ�������130Ԫ/����B�ͳ�ÿ�������200Ԫ/�������������������Ƕ���Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵��������ֱ֪�������ε����Ϊ4����ֱ�DZߵı�Ϊ1��2����б�߳�Ϊ![]() ����ֱ�������ε����߳�Ϊ
����ֱ�������ε����߳�Ϊ![]() ����̱߳�Ϊ1������һ�߳�Ϊ
����̱߳�Ϊ1������һ�߳�Ϊ![]() �����ڡ�ABC�У�����A����B����C=1��5��6�����ABCΪֱ�������Σ��ܵ������������Ϊ12���ױ��ϵĸ�Ϊ4��������Ϊ5��������ȷ���۵�����ǣ�������
�����ڡ�ABC�У�����A����B����C=1��5��6�����ABCΪֱ�������Σ��ܵ������������Ϊ12���ױ��ϵĸ�Ϊ4��������Ϊ5��������ȷ���۵�����ǣ�������
A. ֻ�Т٢ڢ� B. ֻ�Т٢ڢ� C. ֻ�Тۢ� D. ֻ�Тڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶6������б�ҵ���ջ��ݣ�ÿ��3����Ŀ���и質���赸�����Ŀ���꼶ͳ�ƺ��ָ質���Ŀ�����赸���Ŀ����2����6�������赸���Ŀ��![]() ����
����
��1���ú�![]() �Ĵ���ʽ��ʾ:�質���Ŀ��______________����
�Ĵ���ʽ��ʾ:�質���Ŀ��______________����
��2������꼶���ݵĸ質�����赸���Ŀ�����ж��ٸ���
��3����У�ߡ����꼶��СƷ��Ŀ������ݣ��ڸ質���赸��СƷ�����Ŀ�У�ÿ����Ŀ���ݳ�ƽ����ʱ�ֱ���5���ӡ�6���ӡ�8���ӣ�Ԥ��ȫ����Ŀ�������õ�ʱ���ܹ�16���ӣ�����19��00��ʼ��21��30֮ǰ�ݳ��������ʲ����СƷ���Ŀ������ж��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��������ֽƬOABC������ƽ��ֱ������ϵ�У�����A��1��0����C��0��1����PΪAB����һ�����㣬�۵���ֽƬ��ʹO����P���غϣ��ۺ�l��OP���ڵ�M���� �Խ���AC����Q��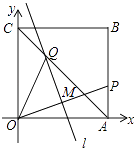
��������P������Ϊ��1�� ![]() �������M�����ꣻ
�������M�����ꣻ
��������P��������1��t��
�����M�����꣨�ú�t��ʽ�ӱ�ʾ����ֱ��д���𰸣�
�����Q�����꣨�ú�t��ʽ�ӱ�ʾ����ֱ��д���𰸣�
������P�ڱ�AB���ƶ�ʱ����QOP�Ķ����Ƿ����仯���������Ϊ�������仯��д�����ĽǶȵĴ�С����˵�����ɣ��������Ϊ�����仯��Ҳ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC=AD����CAD=60�����ֱ�����BC��BD����AEƽ�֡�BAC��BD�ڵ�E����BE=4��ED=8����DF=_____��
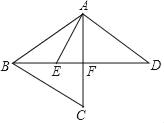
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com