
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.
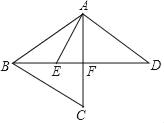
【答案】6
【解析】
连接CE、CD,取DE的中点M,连接CM.首先证明△ECM,△ACD度数等边三角形,再证明△CEF∽△DEC即可解决问题.
解:连接CE、CD,取DE的中点M,连接CM.
∵AB=AC,∠EAB=∠EAC,AE=AE,
∴△EAB≌△EAC,
∴BE=EC=4,∠ABE=∠ACE,
∵AB=AD,
∴∠ABE=∠ADB,
∴∠ACE=∠ADF,
∵∠DFA=∠CFE,
∴∠DAF=∠CEF=60°,
∵EM=ED=4,
∴CE=EM,
∴△EMC是等边三角形,
∴CM=EM=DM,∠EMC=60°,
∵∠EMC=∠MCD+∠MDC,
∴∠MCD=∠MDC=30°,
∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∴∠ADB=∠ABD=∠ACE=∠CDB=30°,
∵∠CEF=∠CED,
∴△CEF∽△DEC,
∴EC2=EFED,
∴16=8EF,
∴EF=2,DF=DE﹣EF=6.
故答案为6.


科目:初中数学 来源: 题型:
【题目】2017年10月31日,在广州举行的世界城市日全球主场活动开幕式上,住建部公布许昌成为“国家生态园林城市”在2018年植树节到来之际,许昌某中学购买了甲、乙两种树木用于绿化校园.若购买7棵甲种树和4棵乙种树需510元;购买3棵甲种树和5棵乙种树需350元.
(1)求甲种树和乙种树的单价;
(2)按学校规划,准备购买甲、乙两种树共200棵,且甲种树的数量不少于乙种树的数量的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D。
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0<a≤4),在平移过程中:
①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?

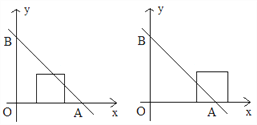
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.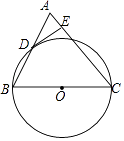
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径等于 ![]() ,cosB=
,cosB= ![]() ,求线段DE的长.
,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A.2种B.3种C.4种D.5种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
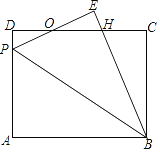
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【题型】解答题
【结束】
25
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的对角线相交于点O,AC= ![]() ,CD=1,
,CD=1,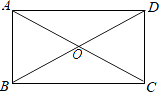
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班40名学生的某次数学测验成绩统计表如下:

(1)若这个班的数学平均成绩是69分,求x和y的值;
(2)设此班40名学生成绩的众数为a分,中位数为b分,求(a-b)2的值;
(3)根据以上信息,你认为这个班的数学水平怎么样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com