
【题目】矩形ABCD的对角线相交于点O,AC= ![]() ,CD=1,
,CD=1,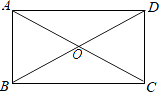
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
【答案】
(1)解:如图所示
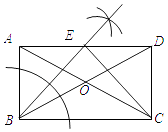
(2)解:BE⊥CE且BE=CE,理由如下:
∵矩形ABCD中,
∴∠BAD=∠ADC=∠ABC=90°,AB=CD,AD∥BC.
∴在Rt△ADH中,AC= ![]() ,CD=1,
,CD=1,
∴ ![]() ,
,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠AEB=∠ABE=45°,
∴AB=AE,
∵AB=CD,
∴AE=AB=1,DE=AD﹣AE=1,
∴AE=DE,
在△ABE与△DCE中, 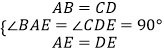 ,
,
∴△DAB≌△DEB(SAS),
∴BE=CE且∠CED=∠AEB=45°.
∴∠BED=180°﹣∠AEB﹣∠CED=90°
∴BE⊥CE且BE=CE.
【解析】(1)根据全等三角形的判定方法作出∠ABC的平分线;(2)根据矩形的性质得到对边平行且相等,四角都等于90°,根据勾股定理求出AD的长,得出△DAB≌△DEB,根据三角形内角和定理,求出∠BED的度数,得到BE⊥CE且BE=CE的结论.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点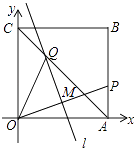
(Ⅰ)若点P的坐标为(1, ![]() ),求点M的坐标;
),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.
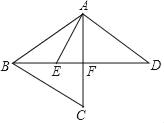
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把任意一个各个数位上的数字均不为0的多位自然数称为“完美数”,若将一个三位“完美数“的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位相加的和,叫做该三位“完美数”的“完美双和”,然后用所得的“完美双和”除以18,得到的结果记为![]() ,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,
,例如“271”是一个三位“完美数”,六个新数为27,21,72,71,12,![]() 则:
则:
![]()
(1)填空:![]() ______;
______;
(2)证明:任意一个三位“完美数”的“完美双和”与该三位“完美数”各数位上数字之差能被21除;
(3)已知一个三位“完美数”![]() 其中
其中![]() ,
,![]() 且x,均为整数
且x,均为整数![]() ,满足百位数字与个位数字之和等于十位数字的2倍加1,求出
,满足百位数字与个位数字之和等于十位数字的2倍加1,求出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
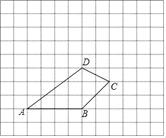
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A′B′C′D′.
(2)求线段AB扫过的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC∥BD,要使△ABC≌△BAD需再补充一个条件,下列条件中,不能选择的是( )
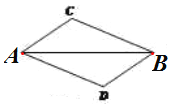
A. BC∥AD B. AC=BD C. BC=AD D. ∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安地震牵动全国人民的心,同学们都在积极进行捐款活动.某校九(2)班同学人人拿出自己的零花钱,踊跃募捐,学生捐款额有5元、10元、15元、20元四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.则该班同学平均捐款 ( )
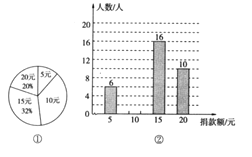
A. 12元 B. 12.5元 C. 13元 D. 13.5元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是( )

A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com