练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，AB=10，AC=2 ，BC边上的高AD=6，则另一边BC等于（ ）
    A.10
    B.8
    C.6或10
    D.8或10

    【答案】C
    【解析】解：根据题意画出图形，如图所示，

    如图1所示，AB=10，AC=2 ，AD=6，

    在Rt△ABD和Rt△ACD中，

    根据勾股定理得：BD= =8，CD= =2，

    此时BC=BD+CD=8+2=10；

    如图2所示，AB=10，AC=2 ，AD=6，

    在Rt△ABD和Rt△ACD中，

    根据勾股定理得：BD= =8，CD= =2，此时BC=BD﹣CD=8﹣2=6，

    则BC的长为6或10．

    所以答案是：C．

    【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点，的坐标分别为，，点是轴上的一个动点，若点关于直线的对称点恰好落在坐标轴上，则点的坐标为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AC=BC，以BC边为直径作⊙O交AB边于点D，过点D作DE⊥AC于点E．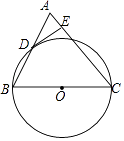

    （1）求证：DE是⊙O的切线；
    （2）若⊙O的半径等于 ，cosB= ，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，P为AD边上一点，沿直线BP将△ABP翻折至△EBP（点A的对应点为点E），PE与CD相交于点O，且OE=OD．

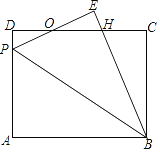
    （1）求证：PE=DH；

    （2）若AB=10，BC=8，求DP的长．

    【答案】（1）见解析；（2）．

    【解析】试题分析：(1) 先证明△DOP≌△EOH，再利用等量代换得到PE=DH.

    (2) 设DP=x， Rt△BCH中，先用 x表示三角形三边，利用勾股定理列式解方程.

    试题解析：

    （1）解：证明：∵OD=OE，∠D=∠E=90°，∠DOP=∠EOH，

    ∴△DOP≌△EOH，

    ∴OP=OH，

    ∴PO+OE=OH+OD，

    ∴PE=DH.

    （2）解：设DP=x，则EH=x，BH=10﹣x，

    CH=CD﹣DH=CD﹣PE=10﹣（8﹣x）=2+x，

    ∴在Rt△BCH中，BC2+CH2=BH2

    （2+x）2+82=（10﹣x）2，

    ∴x=,

    ∴DP=．

    【题型】解答题
    【结束】
    25

    【题目】某文教店老板到批发市场选购A，B两种品牌的绘图工具套装，每套A品牌套装进价比B品牌每套套装进价多2.5元，已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍．

    （1）求A，B两种品牌套装每套进价分别为多少元？

    （2）若A品牌套装每套售价为13元，B品牌套装每套售价为9.5元，店老板决定，购进B品牌的数量比购进A品牌的数量的2倍还多4套，两种工具套装全部售出后，要使总的获利超过120元，则最少购进A品牌工具套装多少套？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（ ）
    A.
    B.
    C.
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

    （1）求证：AF=DC；

    （2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD的对角线相交于点O，AC= ，CD=1，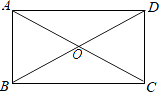

    （1）尺规作图：作∠ABC的平分线交AD于点E，连结CE；
    （2）判断线段BE与CE的关系，并证明你的判断．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB和直线CD相交于O点，OE⊥OD，OF平分∠AOE，∠BOD＝26°

    (1)写出∠COB的邻补角。

    (2)求∠COF的度数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

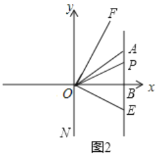
    【题目】已知在平面直角坐标系中，点满足，轴于点．

    （1）点的坐标为 ，点的坐标为 ；

    （2）如图1，若点在轴上，连接，使，求出点的坐标；

    （3）如图2，是线段所在直线上一动点，连接，平分，交直线于点，作，当点在直线上运动过程中，请探究与的数量关系，并证明．

    查看答案和解析>>

    同步练习册答案