
【题目】已知在平面直角坐标系中,点![]() 满足
满足![]() ,
,![]() 轴于点
轴于点![]() .
.

(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;
的坐标为 ;
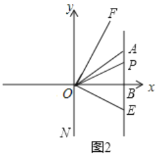
(2)如图1,若点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,使
,使![]() ,求出点
,求出点![]() 的坐标;
的坐标;
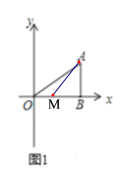
(3)如图2,![]() 是线段
是线段![]() 所在直线上一动点,连接
所在直线上一动点,连接![]() ,
,![]() 平分
平分![]() ,交直线
,交直线![]() 于点
于点![]() ,作
,作![]() ,当点
,当点![]() 在直线
在直线![]() 上运动过程中,请探究
上运动过程中,请探究![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
【答案】(1)(3,2),(3,0);(2)(1,0)或(5,0);(3)2![]() =
=![]() ,理由见详解
,理由见详解
【解析】
(1)根据偶数次幂和二次根式的非负性,求出a,b的值,即可求出A、B的坐标;
(2)根据三角形的面积公式,求出BM的值,进而即可求出M的坐标;
(3)根据平行线的性质得∠EON=∠OEP,根据角平分线的性质得∠EON=∠EOP,进而得∠OEP=∠EOP,结合三角形内角和定理以及垂直的意义,即可得到结论.
(1)∵![]() ,
,
又∵![]() 且
且![]() ,
,
∴![]() ,
,![]() ,即:a=3,b=2,
,即:a=3,b=2,
∴![]() (3,2),
(3,2),
∵![]() 轴于点
轴于点![]() ,
,
∴![]() (3,0).
(3,0).
故答案是:(3,2),(3,0);
(2)∵点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() 轴,
轴,![]() ,如图1,
,如图1,
∴![]() ,即:
,即:![]() ,
,
∴BM=2,
∴点M的坐标为(1,0)或(5,0);
(3)2![]() =
=![]() ,理由如下:
,理由如下:
∵![]() 轴,
轴,
∴AB∥y轴,
∴∠EON=∠OEP,
∵![]() 平分
平分![]() ,
,
∴∠EON=∠EOP,
∴∠OEP=∠EOP=(180°-![]() )÷2,
)÷2,
∵![]() ,
,
∴![]() +∠EOP=90°,
+∠EOP=90°,
∴![]() +
+![]() =90°,即:2
=90°,即:2![]() =
=![]()


科目:初中数学 来源: 题型:
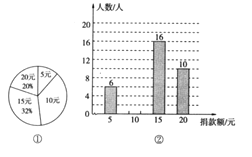
【题目】四川雅安地震牵动全国人民的心,同学们都在积极进行捐款活动.某校九(2)班同学人人拿出自己的零花钱,踊跃募捐,学生捐款额有5元、10元、15元、20元四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.则该班同学平均捐款 ( )
A. 12元 B. 12.5元 C. 13元 D. 13.5元
查看答案和解析>>
科目:初中数学 来源: 题型:
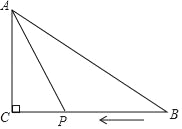
【题目】如图,在三角形ABC中,∠C=90°,AC=6cm,BC=10cm,点P从B点开始向C点运动速度是每秒1cm,设运动时间是t秒,
(1)用含t的代数式来表示三角形ACP的面积.
(2)当三角形ACP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC上的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点![]() 按如图所示的方式叠放在一起(其中
按如图所示的方式叠放在一起(其中![]() ,
,![]() ,
,![]() ),固定三角板
),固定三角板![]() ,另一三角板
,另一三角板![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 顺时针旋转,设旋转的角度为
顺时针旋转,设旋转的角度为![]() .
.
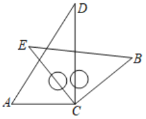
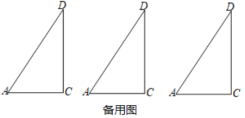
(1)当![]() 时;
时;
①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,求
,求![]() 的度数;
的度数;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() 时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出
时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出![]() 所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,则下列条件中不一定能使△ABC≌△ABD的是( )

A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一假期过后,小明到校后发现忘记带数学课本,一看手表,离上课还有20分钟,他立刻步行返回家中取书,同时,他的父亲也发现小明忘记带数学课本,带上课本立刻以小明步行速度的2倍骑车赶往学校.父子在途中相遇,小明拿到课本后马上按原速步行返回学校,到校后发现迟到了4分钟.如图是父子俩离学校的路程s(米)与所用时间t(分)之间的函数关系,请结合图像,回答下列问题:
(1)两人相遇处离学校的距离是多少米?
(2)试求小明的父亲在赶往学校的过程中,路程s与时间t之间的函数表达式;
(3)假如小明父子相遇拿到课本后,改由他的父亲骑车搭他到学校,他会迟到吗?如果会,迟到几分钟;如果不会,能提前几分钟到校?
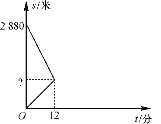
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计). 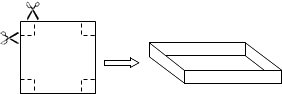
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子. ①要使折成的长方形盒子的底面积为484cm2 , 那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2 , 求此时长方形盒子的长、宽、高(只需求出符合要求的一种情况).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com