
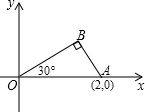
 如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).分析 (1)在Rt△OAB中,由∠AOB=30°可以得到OB=$\sqrt{3}$,过点B作BD垂直于x轴,垂足为D,利用已知条件可以求出OD、BD,也就求出B的坐标;
(2)根据待定系数法把A,B,O三点坐标代入函数解析式中就可以求出解析式;
(3)设存在点C(x,-$\frac{2\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x),过点C作x轴的垂线CE,垂足为E,交OB于点F,则S△OBC=S△OCF+S△BCF,而|CF|=yC-yF=-$\frac{2\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$x=-$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x,这样可以得到S△OBC=-$\frac{\sqrt{3}}{2}$x2+$\frac{3\sqrt{3}}{4}$x,利用二次函数就可以求出△OBC面积最大值,也可以求出C的坐标.
解答 解:(1)在Rt△OAB中,
∵∠AOB=30°,
∴OB=$\sqrt{3}$,
过点B作BD垂直于x轴,垂足为D,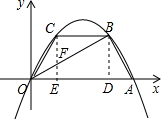 则OD=$\sqrt{3}$cos30°=$\frac{3}{2}$,BD=$\frac{1}{2}$BO=$\frac{\sqrt{3}}{2}$,
则OD=$\sqrt{3}$cos30°=$\frac{3}{2}$,BD=$\frac{1}{2}$BO=$\frac{\sqrt{3}}{2}$,
∴点B的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$);
(2)将A(2,0)、B($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)、O(0,0)三点的坐标代入y=ax2+bx+c,
得:$\left\{\begin{array}{l}{4a+2b+c=0}\\{\frac{9}{4}a+\frac{3}{2}b+c=\frac{\sqrt{3}}{2}}\\{c=0}\end{array}\right.$,
解方程组得$\left\{\begin{array}{l}{a=-\frac{2\sqrt{3}}{3}}\\{b=\frac{4\sqrt{3}}{3}}\\{c=0}\end{array}\right.$.
故所求二次函数解析式是y=-$\frac{2\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x;
(3)设存在点C(x,-$\frac{2\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x)(其中0<x<$\frac{3}{2}$),
过点C作x轴的垂线CE,垂足为E,交OB于点F,
则S△OBC=S△OCF+S△BCF=$\frac{1}{2}$|CF|•|OE|+$\frac{1}{2}$|CF|•|ED|=$\frac{1}{2}$|CF|•|OD|=$\frac{3}{4}$|CF|,
而|CF|=yC-yF=-$\frac{2\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$x=-$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x,
∴S△OBC=-$\frac{\sqrt{3}}{2}$x2+$\frac{3\sqrt{3}}{4}$x=-$\frac{\sqrt{3}}{2}$(x-$\frac{3}{4}$)2+$\frac{9\sqrt{3}}{32}$,
∴当x=$\frac{3}{4}$时,△OBC面积最大,最大面积为$\frac{9\sqrt{3}}{32}$.
此时C点坐标为($\frac{3}{4}$,$\frac{5\sqrt{3}}{8}$).
点评 本题考查了二次函数综合题,涉及到利用待定系数法求解二次函数的解析式,利用二次函数的性质求解函数的最大值等知识,根据题意画出图形,利用数形结合求解是解答此题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:解答题
(1)计算下列算式: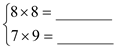 ;
;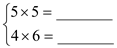 ;
;
(2)从以上的过程中,你发现了什么规律?请用字母表示出来;
(3)请用学过数学知识说明你发现的规律的正确性
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x^2}+2x+1}=x+1$ | B. | $\sqrt{{{(-0.1)}^2}}=0.1$ | C. | $-\sqrt{{{(-\frac{1}{3})}^2}}=\frac{1}{3}$ | D. | ${(-\sqrt{3})^2}=-3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com