
【题目】某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位需0.5万元;新建3个地上停车位和2个地下停车位需1.1万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)若该小区预计投资金额超过10万元而不超过11万元,则共有几种建造方案?
【答案】(1)地上停车场每个0.1万元;地下停车场每个0.4万元;(2)有4种方案:①地上30个,地下20个;②地上31个,地下19个;③地上32个,地下18个;④地上33个,地下17个.
【解析】
(1)设新建一个地上停车位需x万元,新建一个地下停车位需y万元,根据已知新建1个地上停车位和1个地下停车位需5万元;新建3个地上停车位和2个地下停车位需1万元,可列出方程组求解;
(2)设新建m个地上停车位,根据小区预计投资金额超过10万元而不超过11万元,可列出不等式求解.
解:(1)设新建一个地上停车位需x万元,新建一个地下停车位需y万元,由题意得:![]()
解得![]() .
.
答:新建一个地上停车位需0.1万元,新建一个地下停车位需0.4万元.
(2)设新建m个地上停车位,则
10<0.1m+0.4(50-m)≤11,
解得30≤m<![]() ,
,
因为m为整数,所以m=30或m=31或m=32或m=33,
对应的50-m=20或50-m=19或50-m=18或50-m=17,
所以,有四种建造方案.分别是①地上30个,地下20个;②地上31个,地下19个;③地上32个,地下18个;④地上33个,地下17个.


科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系xOy中的点P(a,b)和直线y=ax+b,我们称点P((a,b)是直线y=ax+b的关联点,直线y=ax+b是点P(a,b)的关联直线.特别地,当a=0时,直线y=b(b为常数)的关联点为P(0,b).
如图,已知点A(-2,-2),B(4,-2),C(1,4).
(1)点A的关联直线的解析式为______;
直线AB的关联点的坐标为______;
(2)设直线AC的关联点为点D,直线BC的关联点为点E,点P在y轴上,且S△DEP=2,求点P的坐标.
(3)点M(m,n)是折线段AC→CB(包含端点A,B)上的一个动点.直线l是点M的关联直线,当直线l与△ABC恰有两个公共点时,直接写出m的取值范围.
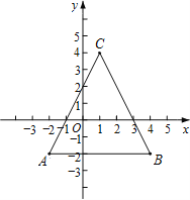
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
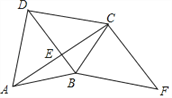
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com