
 如图,二次函数y=x2+m的图形与直线y=2x相交于 A、B两点,且C为顶点.若OA:OB=1:2,求m的值.
如图,二次函数y=x2+m的图形与直线y=2x相交于 A、B两点,且C为顶点.若OA:OB=1:2,求m的值.| AD |
| BE |
| OA |
| OB |
| 1 |
| 2 |
|
 解:作AD⊥y轴于D,BE⊥y轴于E,如图,
解:作AD⊥y轴于D,BE⊥y轴于E,如图,| AD |
| BE |
| OA |
| OB |
| 1 |
| 2 |
|
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |


科目:初中数学 来源: 题型:
 如图所示,南北方向QP为我国的领海线,以西为公海,晚上10点28分,我边防反偷渡巡逻艇122号在A处发现其正西方向有一只可疑船只C之间的距离为10海里,A、B两艇之间的距离为6海里,B艇与可疑船只C之间的距离为8海里,若该可疑船只的速度为12.8海里/时,问该可疑船只最早在何时进入我国领海?
如图所示,南北方向QP为我国的领海线,以西为公海,晚上10点28分,我边防反偷渡巡逻艇122号在A处发现其正西方向有一只可疑船只C之间的距离为10海里,A、B两艇之间的距离为6海里,B艇与可疑船只C之间的距离为8海里,若该可疑船只的速度为12.8海里/时,问该可疑船只最早在何时进入我国领海?查看答案和解析>>
科目:初中数学 来源: 题型:
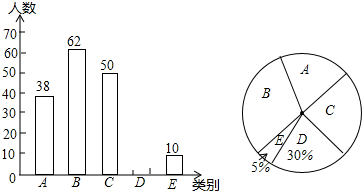
查看答案和解析>>
科目:初中数学 来源: 题型:
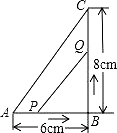 如图,在Rt△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经过多长时间,△PBQ的面积等于6cm2?
如图,在Rt△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经过多长时间,△PBQ的面积等于6cm2?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com