
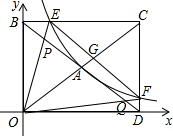
 如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.
如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.分析 (1)①可设F(x,y),可表示出△ODF的面积,可求得k;设出C点坐标为(a,b),可表示出CE、CF,结合A点在反比例函数图象上可求得ab=16,可求得△CEF的面积;②不妨设OD=a,OB=b,可分别表示出DF、FC、BE、CE,可证得$\frac{BE}{CE}$=$\frac{DF}{CF}$;
(2)①可设OD=a,OB=b,可表示出A点坐标和直线BD的解析式,联立直线BD和反比例函数解析式,消去y得到关于x的一元二次方程,利用根的判别式,可判定直线BD与反比例函数图象只有一个交点;②设OD=a,OB=b,可表示出A的坐标,结合条件可求得a=b=4,由条件可证明EF∥BD,由平行线分线段成比例可求得EF的长,此时四边形OBCD为正方形,则AG⊥EF,可知A点关于原点的对称点到EF的距离最小,即为M点,且可求得M点到EF的距离,可求得△MEF的面积.
解答 解:
(1)①设F(x,y)(x>0,y>0),
∵F在反比例函数y=$\frac{k}{x}$上,
∴xy=k,
又S△ODF=$\frac{1}{2}$OD•DF=$\frac{1}{2}$xy=$\frac{1}{2}$k=2,
∴k=4;
设C(a,b),则F(a,$\frac{4}{a}$),E($\frac{4}{b}$,b),
∴CE=a-$\frac{4}{b}$,CF=b-$\frac{4}{a}$,
∵A为OC中点,
∴A点坐标为($\frac{a}{2}$,$\frac{b}{2}$),代入反比例函数解析式可求得ab=16,
∴S△CEF=$\frac{1}{2}$•CE•CF=$\frac{1}{2}$(ab-8+$\frac{16}{ab}$)=$\frac{1}{2}$×(16-8+1)=$\frac{9}{2}$;
②相等.
设OD=a,OB=b,
∵E、F在反比例函数图象上,
∴E($\frac{4}{b}$,b),F(a,$\frac{4}{a}$),
∴BE=$\frac{4}{b}$,DF=$\frac{4}{a}$,
∴CE=BC-BE=OD-BE=a-$\frac{4}{b}$,CF=CD-DF=OB-DF=b-$\frac{4}{a}$,
∴$\frac{BE}{CE}$=$\frac{\frac{4}{b}}{a-\frac{4}{b}}$=$\frac{4}{ab-4}$,$\frac{DF}{CF}$=$\frac{\frac{4}{a}}{b-\frac{4}{a}}$=$\frac{4}{ab-4}$,
∴$\frac{BE}{CE}$=$\frac{DF}{CF}$,
又A为矩形OBCD对角线的交点,
∴A($\frac{a}{2}$,$\frac{b}{2}$),
∴$\frac{a}{2}$×$\frac{b}{2}$=4,解得ab=16,
∴$\frac{BE}{CE}$=$\frac{DF}{CF}$=$\frac{1}{3}$;
(2)①没有.理由如下:
设OD=a,OB=b,
则D(a,0),B(0,b),
∴直线BD解析式为y=-$\frac{b}{a}$x+b,
联立直线BD和反比例函数解析式可得$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=-\frac{b}{a}x+b}\end{array}\right.$,消去y整理可得bx2-abx+4a=0,
△=a2b2-16ab=ab(ab-16),
∵A为线段BD的中点,
∴A($\frac{a}{2}$,$\frac{b}{2}$),且A在反比例函数图象上,
∴ab=16,
∴△=0,
∴bx2-abx+4a=0有两个相等的实数根,
∴双曲线与BD只有一个交点,即A点,
∴除A点外双曲线与BD所在的直线没有其它交点;
②设OD=a,OB=b,
同上可知A($\frac{a}{2}$,$\frac{b}{2}$),且A在反比例函数图象上,
∴ab=16,
又矩形OBCD的周长为16,
∴a+b=8,
解得a=b=4,
∴矩形OBCD为正方形,且D(4,0),B(0,4),A(2,2),
∴OC⊥BD,
又由$\frac{BE}{CE}$=$\frac{DF}{CF}$可得BD∥EF,
∴AG⊥EF,
∴当M点为A点关于原点的对称点时,M到EF的距离最小,
此时M点坐标为(-2,-2),
在Rt△OBD中,由勾股定理可得BD=4$\sqrt{2}$,
∵BD∥EF,
∴$\frac{BE}{BC}$=$\frac{EF}{BD}$,
又E点在反比例函数图象上,
∴E(1,4),
∴CE=1,且BC=4,
∴BE=BC-CE=3
∴$\frac{EF}{BD}$=$\frac{3}{4}$,即$\frac{EF}{4\sqrt{2}}$=$\frac{3}{4}$,
∴EF=3$\sqrt{2}$,且可求得CG=$\frac{3\sqrt{2}}{2}$,
∴AG=AC-CG=2$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$,
∴MG=MA+AG=2OA+AG=4$\sqrt{2}$+$\frac{\sqrt{2}}{2}$=$\frac{9\sqrt{2}}{2}$,
∴S△MEF=$\frac{1}{2}$MG•EF=$\frac{1}{2}$×$\frac{9\sqrt{2}}{2}$×3$\sqrt{2}$=$\frac{27}{2}$,
综上可知存在满足条件的M点,其坐标为(-2,-2),此时△MEF的面积为$\frac{27}{2}$.
点评 本题主要考查反比例函数的综合应用,涉及反比例函数解析式、一元二次方程根的判别式、矩形的性质、平行线分线段成比例等知识点.在(1)①中注意反比例函数中k=xy的应用,在②中注意A在反比例函数图象上的应用;在(2)①中注意利用方程与函数图象的关系把问题转化成一元二次方程根的问题,在②中求得A点坐标判定矩形OBCD为正方形是解题的关键.本题考查知识点较多,综合性很强,难度较大.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:解答题
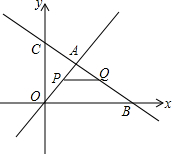 如图,在平面直角坐标系中,两个函数y=x,y=-$\frac{1}{2}$x+6的图象交于点A,动点P从点O开始沿OA方向以每秒$\sqrt{2}$个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设正方形边长为m.|
如图,在平面直角坐标系中,两个函数y=x,y=-$\frac{1}{2}$x+6的图象交于点A,动点P从点O开始沿OA方向以每秒$\sqrt{2}$个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设正方形边长为m.|查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
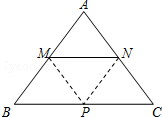 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
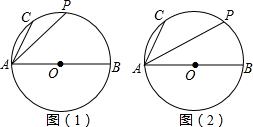
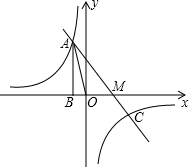 如图,已知反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,一2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,一2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com