
【题目】用总长为6米的铝合金做成一个如图所示的“日”字型窗框,设窗框的高度为x米,窗的透光面积(铝合金所占面积忽略不计)为y平方米.
(1)求y与x之间的函数关系式(结果要化成一般形式);
(2)能否使窗的透光面积达到2平方米,如果能,窗的高度和宽度各是多少?如果不能,试说明理由;
(3)窗的高度为多少时,能使透光面积最大?最大面积是多少?
【答案】
(1)解:设窗框的长为x米,则宽为 ![]() (6﹣2x)米,
(6﹣2x)米,
窗户的透光面积为:y=x ![]() (6﹣2x)=﹣
(6﹣2x)=﹣ ![]() x2+2x
x2+2x
(2)解:令y=2得:2=﹣ ![]() x2+2x,整理得:2x2﹣6x+6=0,
x2+2x,整理得:2x2﹣6x+6=0,
∵△=b2﹣4ac=﹣12<0,
∴此方程无解,
∴不能使窗的透光面积达到2平方米
(3)解:∵y=﹣ ![]() x2+2x=﹣
x2+2x=﹣ ![]() (x﹣1.5)2+1.5,
(x﹣1.5)2+1.5,
∵a=﹣ ![]() <0,
<0,
∴y有最大值,当x=1.5时,y的最大值是1.5.
答:窗的高度1.5米时,能使透光面积最大,最大面积是1.5米2
【解析】(1)设窗框的长为x米,则宽为 ![]() (6﹣2x)米,进而得出函数关系式即可;(2)令y=2,代入函数关系式,则可判定所对应方程根的判别式和0的大小即可;(2)根据面积公式列出二次函数解析式,用配方法求其最大值即可.
(6﹣2x)米,进而得出函数关系式即可;(2)令y=2,代入函数关系式,则可判定所对应方程根的判别式和0的大小即可;(2)根据面积公式列出二次函数解析式,用配方法求其最大值即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小红做一道数学题“两个多项式A,B,B为![]() ,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为
,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为![]() .
.
(1)你能求出多项式A吗?
(2)试求A+2B的正确结果;
(3)求出当![]() 时A+2B的值.
时A+2B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2-6x-1=0时,方程可变形为( )
A. (x-3)2=10 B. (x-6)2=37 C. (x-3)2=4 D. (x-3)2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家“精准扶贫”号召,某银行2018年安排精准扶贫贷款100亿元,已知该银行2016年安排精准扶贫贷款64亿元,设2016年至2018年该银行安排精准扶贫贷款的平均增长率为x,根据题意可列方程为( )
A.100(1+x)2=64B.64(1+x)2=100
C.64(1+2x)=100D.64(1﹣x2)=100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨2000元的原料运回工厂,制成每吨7500元的产品运到B地.已知公路运价为2元/ (吨·千米),铁路运价为 1.5元/(吨·千米),且这两次运输共支出公路运输费2.6万元,铁路运输费15.6万元。
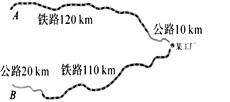
求:(1)该工厂从A地购买了多少吨原料? 制成运往B地的产品多少吨?
(2)若不计人力成本,这批产品盈利多少元? (盈利=销售款-原料费-运输费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读新知:移项且合并同类项之后,只含有偶次项的四次方程称作双二次方程.其一般形式为ax4+bx2+c=0(a≠0),一般通过换元法解之,具体解法是设 x2=y,则原四次方程化为一元二次方程:ay2+by+c=0,解出y之后代入x2=y,从而求出x的值.例如解:4x4﹣8y2+3=0
解:设x2=y,则原方程可化为:4y2﹣8y+3=0
∵a=4,b=﹣8,c=3
∴b2﹣4ac=﹣(﹣8)2﹣4×4×3=16>0
∴y= ![]() =
= ![]()
∴y1= ![]() ,
,
∴y2= ![]()
∴当y1= ![]() 时,x2=
时,x2= ![]()
∴x1= ![]() ,x2=﹣
,x2=﹣ ![]() ;当y1=
;当y1= ![]() 时,x2=
时,x2= ![]()
∴x3= ![]() ,x4=﹣
,x4=﹣ ![]()
小试牛刀:请你解双二次方程:x4﹣2x2﹣8=0
归纳提高:思考以上解题方法,试判断双二次方程的根的情况,下列说法正确的是(选出所有的正确答案)
①当b2﹣4ac≥0时,原方程一定有实数根;②当b2﹣4ac<0时,原方程一定没有实数根;③当b2﹣4ac≥0,并且换元之后的一元二次方程有两个正实数根时,原方程有4个实数根,换元之后的一元二次方程有一个正实数根一个负实数根时,原方程有2个实数根;④原方程无实数根时,一定有b2﹣4ac<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com