
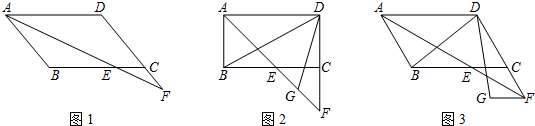
分析 (1)根据等边对等角∠CEF=∠F,利用四边形ABCD是平行四边形,可得∠FAD=∠FEC∠BAF=∠F,等量关系可得∠BAF=∠DAF,即可求解.
(2)根据∠ABC=90°,G是EF的中点可直接求得.
(3)延长AB,FG相较于H,连接EG,DH,求证四边形CEGF是平行四边形,再求证△AHD、△FHD是等边三角形,求证△BHD≌△GFD,即可求得答案.
解答 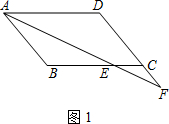 (1)证明:如图1,∵CE=CF
(1)证明:如图1,∵CE=CF
∴∠CEF=∠F,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴∠FAD=∠FEC,∠BAF=∠F,
∴∠BAF=∠FAD,
∴AF是∠BAD的平分线; 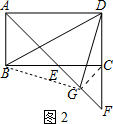 (2)解:如图2,连接CG,BG
(2)解:如图2,连接CG,BG
在平行四边形ABCD中,∠ABC=90°,
∴平行四边形ABCD是矩形,
∴AD=BC,∠BCD=90°,
∴∠BCF=180°-90°=90°,
又∵CE=CF,
∴△CEF是等腰直角三角形,即:∠CEF=∠F=45°,
由(1)可得:∠FAD=∠CEF=∠F=45°,
∴AD=DF=BC,
又∵G是EF的中点,
∴CG=GF,∠ECG=∠F=45°,∠CGF=90°,
在△BGC与△DGF中,
$\left\{\begin{array}{l}{DF=BC}\\{∠ECG=∠F}\\{CG=GF}\end{array}\right.$,
∴△BGC≌△DGF(SAS),
∴BG=DG,∠BGC=∠DGF,
∴∠BGD=∠CGF=90°
∴△BGD是等腰直角三角形,即:∠BDG=45°;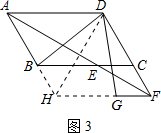 (3)解:如图3,延长AB,FG相较于H,连接EG,DH.
(3)解:如图3,延长AB,FG相较于H,连接EG,DH.
∴GF∥CE,GF=CE
∴四边形EGFC是平行四边形.
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形
由(1)可得:AD=DF,CE=CF
∴平行四边形EGFC是菱形.平行四边形AHFD是菱形.
∵∠BAD=60°
∴△AHD、△FHD是等边三角形,即∠ADH=∠FDH=60°,
在△BHD与△GFD中,
$\left\{\begin{array}{l}{DH=DF}\\{∠BHD=∠GFE}\\{BH=GF}\end{array}\right.$,
∴△BHD≌△GFD(SAS),
∠BDH=∠GDF,
∴∠BDG=60°.
点评 此题主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.同学们在解决此类问题时,可以通过以下的步骤进行思考和分析:(1)通过测量或特殊情况的提示进行猜想;(2)根据猜想的结果进行联想(如60度角可以联想到等边三角形,45度角可以联想到等腰直角三角形等);(3)在联想的基础上根据已知条件利用几何变换(如旋转、平移、轴对称等)构造全等解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
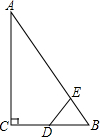 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为2或3.5.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为2或3.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
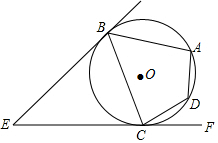 如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是( )
如图,EB,EC是⊙O的两条切线,与⊙O相切于B,C两点,点A,D在圆上.若∠E=46°,∠DCF=32°,则∠A的度数是( )| A. | 102° | B. | 99° | C. | 92° | D. | 67° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7cm、5cm、12cm | B. | 6cm、8cm、15cm | C. | 8cm、4cm、3cm | D. | 4cm、6cm、5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2(x+2)2+1 | B. | y=2(x-2)2+1 | C. | y=2(x+2)2-1 | D. | y=2(x-2)2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com