Question

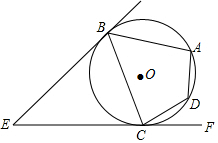
15．如图，EB，EC是⊙O的两条切线，与⊙O相切于B，C两点，点A，D在圆上．若∠E=46°，∠DCF=32°，则∠A的度数是（　　）

• A． 102°
• B． 99°
• C． 92°
• D． 67°

Answer 1

分析 先根据切线长定理得到EB=EC，则∠ECB=∠EBC，于是可根据三角形内角和定理可计算出∠ECB=$\frac{1}{2}$（180°-∠E）=67°，接着利用平角的定义可计算出∠BCD=180°-∠ECB-∠DCF=81°，然后根据圆内接四边形的性质计算∠A的度数．

解答 解：∵EB，EC是⊙O的两条切线，
∴EB=EC，
∴∠ECB=∠EBC，
∴∠ECB=$\frac{1}{2}$（180°-∠E）=$\frac{1}{2}$×（180°-46°）=67°，
∴∠BCD=180°-∠ECB-∠DCF=180°-67°-32°=81°，
∵四边形ABCD为⊙O的内接四边形，
∴∠A+∠BCD=180°，
∴∠A=180°-81°=99°．
故选B．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径；从圆外一点引圆的切线，切线长相等．也考查了圆内接四边形的性质．