
【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF 
(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
【答案】
(1)证明:连接DB,CF,
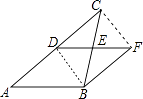
∵DE是△ABC的中位线,
∴CE=BE,
∵EF=ED,
∴四边形CDBF是平行四边形,
∴CD=BF
(2)证明:∵四边形CDBF是平行四边形,
∴CD∥FB,
∴AD∥BF,
∵DE是△ABC的中位线,
∴DE∥AB,
∴DF∥AB,
∴四边形ABFD是平行四边形
【解析】(1)连接DB,CF,利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形,进而可得CD=BF;(2)由(1)可得CD∥FB,再利用三角形中位线定理可得DF∥AB,根据两组对边分别平行的四边形是平行四边形可得结论.
【考点精析】利用三角形中位线定理和平行四边形的判定对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


科目:初中数学 来源: 题型:
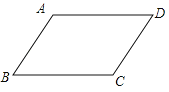
【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
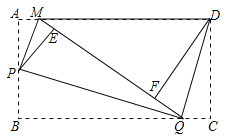
【题目】如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
根据以上信息解决下列问题:
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | 20 |
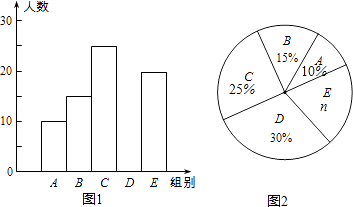
(1)在统计表中,m= , n= , 并补全直方图;
(2)扇形统计图中“C组”所对应的圆心角的度数是度;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中(AB>AC),AH⊥BC,垂足为H,E、D、F分别是各边的中点,则四边形EDHF是( ) 
A.梯形
B.等腰梯形
C.直角梯形
D.矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,AH⊥BC于H,E,D,F分别是AB,BC,AC的中点,则四边形EDHF是( ) 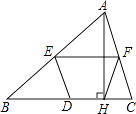
A.一般梯形
B.等腰梯形
C.直角梯形
D.直角等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某地七年级男生的身高情况,从当地某学校选取了一个容量为60的样本,60名男生的身高(单位:cm)情况如下表所示(尚不完整),则表中a,b的值分别为( )
分组 | 147.5~157.5 | 157.5~167.5 | 167.5~177.5 | 177.5~187.5 |
频数 | 10 | 26 | a | |
百分比 | 30% | b |
A. 18,6 B. 30%,6 C. 18,10% D. 0.3,10%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com