
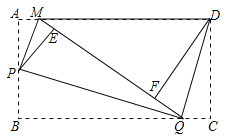
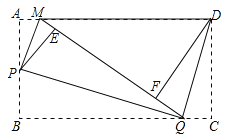
【题目】如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
【答案】(1)△AMP∽△BPQ∽△CQD;(2)AB=6.
【解析】
试题分析:(1)由矩形的性质得∠A=∠B=∠C=90°,由折叠的性质和等角的余角相等,可得∠BPQ=∠AMP=∠DQC,所以△AMP∽△BPQ∽△CQD;
(2)先证明MD=MQ,然后根据sin∠DMF=![]() =
=![]() ,设DF=3x,MD=5x,表示出AP、BP、BQ,再根据△AMP∽△BPQ,列出比例式解方程求解即可.
,设DF=3x,MD=5x,表示出AP、BP、BQ,再根据△AMP∽△BPQ,列出比例式解方程求解即可.
试题解析:(1)△AMP∽△BPQ∽△CQD,∵四边形ABCD是矩形,∴∠A=∠B=∠C=90°,根据折叠的性质可知:∠APM=∠EPM,∠EPQ=∠BPQ,∴∠APM+∠BPQ=∠EPM+∠EPQ=90°,∵∠APM+∠AMP=90°,∴∠BPQ=∠AMP,∴△AMP∽△BPQ,同理:△BPQ∽△CQD,根据相似的传递性,△AMP∽△CQD;
(2)∵AD∥BC,∴∠DQC=∠MDQ,根据折叠的性质可知:∠DQC=∠DQM,∴∠MDQ=∠DQM,∴MD=MQ,∵AM=ME,BQ=EQ,∴BQ=MQ﹣ME=MD﹣AM,∵sin∠DMF=![]() =
=![]() ,∴设DF=3x,MD=5x,∴BP=PA=PE=
,∴设DF=3x,MD=5x,∴BP=PA=PE=![]() ,BQ=5x﹣1,∵△AMP∽△BPQ,∴
,BQ=5x﹣1,∵△AMP∽△BPQ,∴![]() ,∴
,∴ ,解得:
,解得:![]() (舍)或x=2,∴AB=6.
(舍)或x=2,∴AB=6.


科目:初中数学 来源: 题型:
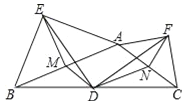
【题目】如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读材料,获取新知】
善于思考的小军在解方程组![]() 时,采用了一种“整体代换法”的解法.
时,采用了一种“整体代换法”的解法.
解:将方程(2)变形:4x+10y+y=5即2(2x+5y)+y=5(3)
把方程(1)代入(3)得:2×3+y=5
∴y=﹣1.
把y=﹣1,代入(1)得x=4
∴方程组的解为 ![]()
【利用新知,解答问题】
请你利用小军的“整体代换法”解决一下问题:
(1)解方程组:
① ![]() ②
② 
(2)已知x,y满足方程组 ![]() ,则x2+4y2与xy的值分别为、 .
,则x2+4y2与xy的值分别为、 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,D、E、F分别为AB、BC、AC边上的中点,AC=4cm,BC=6cm,那么四边形CEDF为 , 它的边长分别为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com