【题目】如图所示，△ABC中，AH⊥BC于H，E，D，F分别是AB，BC，AC的中点，则四边形EDHF是（ ）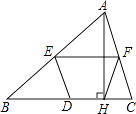 
A.一般梯形
B.等腰梯形
C.直角梯形
D.直角等腰梯形
【答案】B
【解析】解：在△ABC中，E，F分别是AB，AC的中点，∴EF= 
BC，∴EF∥BC，又∵E，D分别是AB，BC的中点，∴ED= AC，
∵AH⊥BC，F是AC的中点，∴HF= AC，
∴ED=HF，
∵EF∥DH，ED=HF且ED不平行HF，
∴四边形EDHF是等腰梯形，
故选B．
【考点精析】关于本题考查的三角形中位线定理和等腰梯形的判定，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；两腰相等的梯形是等腰梯形；同一底上的两个角相等的梯形是等腰梯形；两条对角线相等的梯形是等腰梯形才能得出正确答案．
科目：初中数学 来源： 题型：
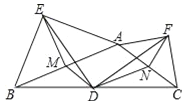
【题目】如图，在钝角△ABC中，点D是BC的中点，分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF，M、N分别为AB、AC的中点，连接DM、DN、DE、DF、EM、EF、FN．求证：
（1）△EMD≌△DNF；
（2）△EMD∽△EAF；
（3）DE⊥DF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠C=90°，D、E、F分别为AB、BC、AC边上的中点，AC=4cm，BC=6cm，那么四边形CEDF为 ， 它的边长分别为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售一批衬衫， 平均每天可售出20件，每件赢利40元，为了扩大销售,增加盈利，尽快减少库存,商场决定采取适当降价措施经调查发现，如果每件衬衫每降价一元，商场平均每天可多售出2件.若商场平均每天赢利1200元,每件衬衫应降价______元.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将抛物线y＝3x2先向右平移1个单位长度，再向上平移4个单位长度，平移后抛物线的函数表达式是( )
A. y＝3(x+1)2+4B. y＝3(x﹣1)2+4
C. y＝3(x+1)2﹣4D. y＝3(x﹣1)2﹣4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在□ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是( ) ．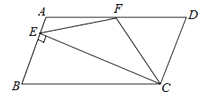
①∠DCF=∠BCD；②EF=CF；③S△BEC ＝2S△CEF；④∠DFE=3∠AEF．
A.①②③
B.①③
C.①②④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
