
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

【答案】(1)150°;(2)2
【解析】分析:(1)先根据三角形内角和计算出∠BAC=150°,然后利用旋转的定义可判断旋转中心为点A,旋转角为150°;(2)根据旋转的性质得到∠DAE=∠BAC=150°,AB=AD=4,AC=AE,利用周角定义可得到∠BAE=60°,然后利用点C为AD中点得到AC=![]() AD=2,于是得到AE=2.
AD=2,于是得到AE=2.
本题解析:
解:(1)在△ABC中,∵∠B+∠ACB=30°, ∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE, ∴∠BAE=360°-150°-150°=60°,
∵点C为AD中点, ∴AC=![]() AD=2, ∴AE=2.
AD=2, ∴AE=2.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
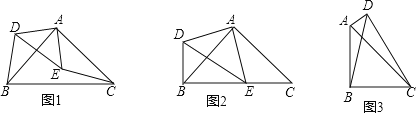
【题目】问题背景:某数学兴趣小组把两个等腰直角三角形的直角顶点重合,发现了一些有趣的结论.
结论一:
(1)如图1,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE,试说明△ADB≌△AEC;
结论二:
(2)如图2,在(1)的条件下,若点E在BC边上,试说明DB⊥BC;
应用:
(3)如图3,在四边形ABCD中,∠ABC=∠ADC=90°,AB=CB,∠BAD+∠BCD=180°,连接BD,BD=7cm,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另行收费,甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),则点A,B的对应点A1,B1的坐标分别为 ;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
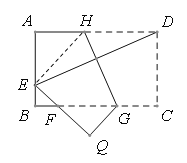
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
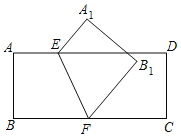
【题目】如图,点E、F分别在矩形ABCD的边AD、AB上,连接EF,四边形ABFE沿EF翻折能与四边形![]() 重合,且
重合,且![]() 与ED相交,若
与ED相交,若![]() ,则
,则![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com