
| A种产品 | B种产品 | |
| 成本(万元╱件) | 2 | 5 |
| 利润(万元╱件) | 1 | 3 |
分析 (1)设生产A种产品x件,则生产B种产品有(10-x)件,根据计划获利14万元,即两种产品共获利14万元,即可列方程求解;
(2)根据计划投入资金不多于26万元,这两个不等关系即可列出不等式,求得x的范围,再根据x是非负整数,确定x的值,x的值的个数就是方案的个数.
解答 解:(1)设生产A产品x件,B产品y件.
由题意得:$\left\{\begin{array}{l}x+y=10\\ x+3y=14\end{array}\right.$,
解这个方程得:$\left\{\begin{array}{l}x=8\\ y=2\end{array}\right.$,
答:若工厂计划获利14万元,生产A产品8件,B产品2件.
(2)设生产A产品z件
由题意得:2z+5(10-z)≤26,
解得:z≥8.
因为8≤z≤10,且z为整数.
所以z=8,z=9,z=10.
方案一:生产A产品8件,B产品2件
方案二:生产A产品9件,B产品1件
方案三:生产A产品10件.
点评 本题考查了二元一次方程的应用,一元一次不等式的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的数量关系.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $2+\sqrt{2}=2\sqrt{2}$ | C. | $\sqrt{6}÷2=\sqrt{3}$ | D. | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
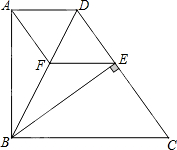 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.
如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
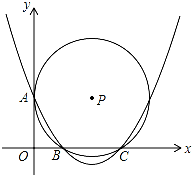 已知:如图,在平面直角坐标系xOy中,点A(0,$\sqrt{3}$),点B(1,0),点C(3,0),以点P为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).
已知:如图,在平面直角坐标系xOy中,点A(0,$\sqrt{3}$),点B(1,0),点C(3,0),以点P为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com