
分析 根据正数>负数,两个负数,绝对值大的反而小,即可解答.
解答 解:(1)∵$\frac{1}{2}>\frac{1}{3}$,
∴$-\frac{1}{2}<-\frac{1}{3}$;
(2)∵-|-5|=-5,6>5,
∴-6<-|-5|;
(3)-|-$\frac{2}{5}$|=-$\frac{2}{5}$,$-|-\frac{3}{2}|=-\frac{3}{2}$,
∵$\frac{2}{5}<\frac{3}{2}$,
∴$-\frac{2}{5}>-\frac{3}{2}$,
∴$-|-\frac{2}{5}|>-|-\frac{3}{2}|$;
(4)3.1×106=3100000,3.12×105=312000,
∴3.1×106>3.12×105;
(5)∵3.6×106<3.61×106,
∴-3.6×106>3.61×106
故答案为:(1)<;(2)<;(3)>;(4)>;(5)>.
点评 本题考查了有理数比较大小,解决本题的关键是明确正数>负数,两个负数,绝对值大的反而小.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
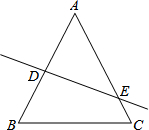 如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.
如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有理数a、b、c在数轴上的位置如图所示,且表示数a的点与表示数b的点到原点的距离相等
有理数a、b、c在数轴上的位置如图所示,且表示数a的点与表示数b的点到原点的距离相等查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com