
���� ��1����ͼ1����EQ��AB����BC�ڵ�Q������֤����BFD�ա�QFE��ASA�����Ӷ���֤��BD=CE����AD=AB+EC��Ȼ����FG��AB����AC�ڵ�G��֤��FG�ǡ�ADE����λ�ߵõ�FG=$\frac{1}{2}AD$��Ȼ����֤��FG=FC���ɣ�
��2����ͼ2����EQ��AB����BC�ڵ�Q����֤����BFD�ס�QFE��ASA�����Ӷ��õ�CE=$\sqrt{3}$BD����FG��AB����AC�ڵ�G����EF=$\sqrt{3}$DF����֪$\frac{FG}{AD}$=$\frac{\sqrt{3}}{\sqrt{3}+1}$���Ӷ���֤��FG=$\frac{3-\sqrt{3}}{2}$��AB+$\frac{\sqrt{3}}{3}$CE������ΪFG=CF���ʴ�CF=$\frac{3-\sqrt{3}}{2}$AB+$\frac{\sqrt{3}-1}{2}$CE��
��3����ͼ3������F��FG��AB������ΪG����FC=6��EC=3$\sqrt{3}$-3������CF=$\frac{3-\sqrt{3}}{2}$AB+$\frac{\sqrt{3}-1}{2}$CE�ã�AB=3$\sqrt{3}$+3��Ȼ�����BF�ij��ȣ��Ӷ���֪BF=EC��Ȼ��֤����ABF�ա�BCE���ɵõ���EBC=��BAF����������Rt��BGF�пɿ����GB��GF�ij���Ȼ�������AG�ij����������Rt��AGF�У����AF=3$\sqrt{6}$��Ȼ����֤����BFN�ס�BFA�������������ε����ʿ�֪�����BN=$\sqrt{6}$��NF=2$\sqrt{6}$-3$\sqrt{2}$���ʴ�NE2$\sqrt{6}$����Rt��EMN�У���MEN=30�㣬����MN=$\frac{1}{2}EN$=$\sqrt{6}$���ʴ�BN=NM���ɡ�MBN=��BMN����MBN+��BMN=��MNE=60�㣬��֪��MBN=30�㣬����tan��MBN=$\frac{\sqrt{3}}{3}$��
��� �⣺��1����ͼ1����EQ��AB����BC�ڵ�Q��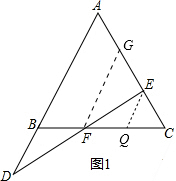
��EQ��AB��
���BDF=��QEF����BFE=��QFE��
��DF=EF��
�ڡ�BFD�͡�QFE�У�
$\left\{\begin{array}{l}{��BDF=��QEF}\\{DF=EF}\\{��BFE=��QFE}\end{array}\right.$��
���BFD�ա�QFE��ASA����
��BD=EQ��
�ߡ�ABC�ǵȱ������Σ�
���EQCҲ�ǵȱ������Σ�
��EQ=CE��
��BD=CE��
��FG��AB����AC�ڵ�G��
��DF=EF��
��FG��ADE����λ�ߣ�
��2FG=AB+BD��
�ߡ�GFC�ǵȱ������Σ�
��FG=CF��
��2CF=AB+BD������CF=AB+CE��
��2CF-CE=AB��
��2����ͼ2����EQ��AB����BC�ڵ�Q��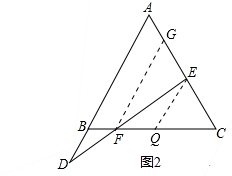
��EQ��AB��
���BDF=��QEF����BFE=��QFE��
���BFD�ס�QFE��ASA����
��EF=$\sqrt{3}$DF��
��EQ=$\sqrt{3}$BD��
�ߡ�ABC�ǵȱ������Σ�
���EQCҲ�ǵȱ������Σ�
��EQ=CE��
��CE=$\sqrt{3}$BD��
��FG��AB����AC�ڵ�G��
��EF=$\sqrt{3}$DF��
��$\frac{FG}{AD}$=$\frac{\sqrt{3}}{\sqrt{3}+1}$��
��FG=$\frac{3-\sqrt{3}}{2}$��AB+BD������FG=$\frac{3-\sqrt{3}}{2}$��AB+$\frac{\sqrt{3}}{3}$CE����
�ߡ�GFC�ǵȱ������Σ�
��FG=CF��
��CF=$\frac{3-\sqrt{3}}{2}$��AB+$\frac{\sqrt{3}}{3}$CE������CF=$\frac{3-\sqrt{3}}{2}$AB+$\frac{\sqrt{3}-1}{2}$CE��
�ʴ�Ϊ��CF=$\frac{3-\sqrt{3}}{2}$AB+$\frac{\sqrt{3}-1}{2}$CE��
��3����ͼ3������F��FG��AB������ΪG��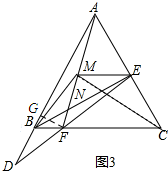
��FC=6��EC=3$\sqrt{3}$-3������CF=$\frac{3-\sqrt{3}}{2}$AB+$\frac{\sqrt{3}-1}{2}$CE�ã�AB=3$\sqrt{3}$+3��
��BF=BC-FC=3$\sqrt{3}$-3��
��BF=EC��
�ڡ�ABF�͡�BCE�У�
$\left\{\begin{array}{l}{AB=CB}\\{��ABF=��BCE}\\{BF=CE}\end{array}\right.$��
���ABF�ա�BCE��
���EBC=��BAF��
��FG��AB����GBF=60�㣬
��GB=$\frac{1}{2}BF$=$\frac{3\sqrt{3}-3}{2}$��FG=$\frac{9-3\sqrt{3}}{2}$��
��AG=AB-BG=$\frac{3\sqrt{3}+9}{2}$��
��Rt��AGF��AF=$\sqrt{A{G}^{2}+F{G}^{2}}$=$\sqrt{��\frac{3\sqrt{3}+9}{2}��^{2}+��\frac{9-3\sqrt{3}}{2}��^{2}}$=3$\sqrt{6}$��
�ڡ�BFN�͡�BFA�У�$\left\{\begin{array}{l}{��EBC=��BAF}\\{��BFN=��BFA}\end{array}\right.$��
���BFN�ס�BFA��
��$\frac{BN}{AB}=\frac{FN}{BF}=\frac{BF}{AF}$������$\frac{BN}{3\sqrt{3}+3}=\frac{FN}{3\sqrt{3}-3}=\frac{3\sqrt{3}-3}{3\sqrt{6}}$��
��ã�BN=$\sqrt{6}$��NF=2$\sqrt{6}$-3$\sqrt{2}$��
��NE=BE-BN=AF-BN=2$\sqrt{6}$��
�ߡ�BFN�ס�BFA��
���BNF=��ABF=60�㣮
���MNE=60�㣮
���MEN=30�㣮
��Rt��EMN�У���MEN=30�㣬
��MN=$\frac{1}{2}EN$=$\frac{1}{2}��2\sqrt{6}$=$\sqrt{6}$��
��BN=NM��
���MBN=��BMN��
�֡ߡ�MBN+��BMN=��MNE=60�㣬
���MBN=30�㣮
��tan��MBN=$\frac{\sqrt{3}}{3}$��
���� ������Ҫ����������������ε����ʺ��ж���ȫ�������ε����ʺ��ж������ɶ�����Ӧ�ã�����������Ǻ���ֵ�����������ε����ʺ��ж������AF��NB��MN�ij��ȣ��Ӷ��õ���MBN=30���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
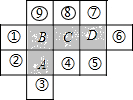 ��ͼ���������֢١�����������������ĸA��B��C��D�������δ�С����ͬ���ִӱ������ֵ�9���������еȿ��ܵ���ѡһ��������ѡ�������������ĸ������������ɵ�ͼ��ǡ������һ���ǵ�������ı���չ��ͼ����û�иǵ�һ��ǡ���������ĸ��A����һ����Եĸ���Ϊ ��������
��ͼ���������֢١�����������������ĸA��B��C��D�������δ�С����ͬ���ִӱ������ֵ�9���������еȿ��ܵ���ѡһ��������ѡ�������������ĸ������������ɵ�ͼ��ǡ������һ���ǵ�������ı���չ��ͼ����û�иǵ�һ��ǡ���������ĸ��A����һ����Եĸ���Ϊ ��������| A�� | $\frac{4}{9}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{9}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
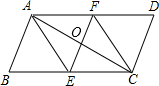 ��ͼ����?ABCD�У�AE��CF�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ��ֱ�BC��AD�ڵ�E��F������AC��EF�ཻ�ڵ�O������E��BC���е㣬AB��AC��AB=2�����ı���AECF�������2$\sqrt{3}$��
��ͼ����?ABCD�У�AE��CF�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ��ֱ�BC��AD�ڵ�E��F������AC��EF�ཻ�ڵ�O������E��BC���е㣬AB��AC��AB=2�����ı���AECF�������2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com