练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．若m+n=-1，则（m+n）2-2m-2n的值为3．

    分析 把（m+n）看作一个整体并直接代入代数式进行计算即可得解．

    解答 解：∵m+n=-1，
    ∴（m+n）2-2m-2n=（m+n）2-2（m+n），
    =（-1）2-2×（-1），
    =1+2，
    =3．
    故答案为：3．

    点评 本题考查了代数式求值，整体思想的利用是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．已知$\frac{x}{{x}^{2}-x+1}$=2，求$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．当x≥8时，$\sqrt{x-8}$是二次根式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

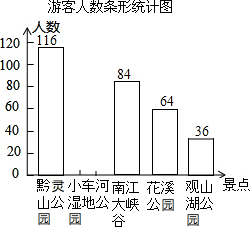    12．近年来，随着创建“生态文明城市”活动的开展，我市的社会知名度越来越高，吸引了很多外地游客，某旅行社对5月份本社接待外地游客来我市各景点旅游的人数作了一次抽样调查，并将调查结果绘制成如下两幅不完整的统计图表：
    游客人数统计表
    景点频数（人数）频率
    黔灵山公园1160.29
    小车河湿地公园0.25
    南江大峡谷840.21
    花溪公园640.16
    观山湖公园360.09
    （1）此次共调查400人，并补全条形统计图；
    （2）由上表提供的数据可以制成扇形统计图，求“南江大峡谷”所对的圆心角的度数；
    （3）该旅行社预计7月份接待来我市的游客有2500人，根据以上信息，请你估计去黔灵山公园的游客大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

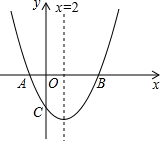    19．如图，经过点C（0，-4）的抛物线y=ax2+bx+c（a≠0）与x轴相交于A（-2，0），B两点．
    （1）a＞0，b2-4ac＞0（填“＞”或“＜”）；
    （2）若该抛物线关于直线x=2对称，求抛物线的函数表达式；
    （3）在（2）的条件下，连接AC，E是抛物线上一动点，过点E作AC的平行线交x轴于点F．是否存在这样的点E，使得以A，C，E，F为顶点所组成的四边形是平行四边形？若存在，求出满足条件的点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．抛物线y=ax2（a≠0）是一条不经过一、二象限的抛物线，则点（-a，a-1）在第四象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：等边△ABC中，D是射线AB上的点，点E是边AC上的点，线段DE交BC于F．
    （1）如图1，若DF=EF，求证：2CF-CE=AB；
    （2）如图2，若EF=$\sqrt{3}$DF，直接写出CF、CE、AB之间的数量关系CF=$\frac{3-\sqrt{3}}{2}$AB+$\frac{\sqrt{3}-1}{2}$CE；
    （3）在②的条件下，连接AF、BE，BE与AF交于点N，过点E作EM⊥AF，垂足为M，连接BM、MC，若FC=6，EC=$3\sqrt{3}-3$，求线段tan∠MBN的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

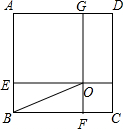    18．如图，在正方形ABCD中，点E、F、G、H分别在四边上，EH∥BC，GF∥AB，EH与FG交于点O，且AE=AG，若AE比CH长2，△BOF的面积为$\frac{3}{2}$
    （1）求正方形ABCD的面积；
    （2）设AE=a，BE=b，求代数式a4+b4的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若x-y=2，x-z=3，则（y-z）2-3（z-y）+9的值为（　　）
    A．13B．11C．5D．7

    查看答案和解析>>

    同步练习册答案