
【题目】已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC. 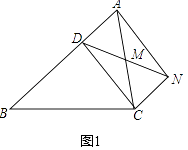
(1)求证:四边形ADCN是平行四边形.
(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外) 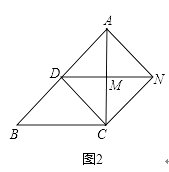
【答案】
(1)证明:∵CN∥AB,
∴∠DAM=∠NCM,
在△ADM和△CNM中,
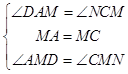 ,
,
∴△AMD≌△CMN(ASA),
∴MD=MN,
∴四边形ADCN是平行四边形
(2)解:∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MC=MD,
∴AC=DN,
∴ADCN是矩形,
∵AC=BC,
∴AD=BD,
∵∠ACB=90°,
∴CD=AD=BD= ![]() AB,
AB,
∴ADCN是正方形,
∴AN=AD=BD=CD=CN.
【解析】(1)由CN∥AB,MA=MC,易证得△AMD≌△CMN,则可得MD=MN,即可证得:四边形ADCN是平行四边形.(2)由∠AMD=2∠MCD,可证得四边形ADCN是矩形,又由∠ACB=90°,AC=BC,可得四边形ADCN是正方形,继而求得答案.
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.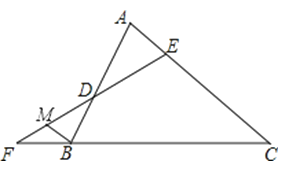
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.相等的角是对顶角
B.两条直线被第三条直线所截,同位角相等
C.在同一平面内,垂直于同一条直线的两条直线平行
D.同旁内角互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com