
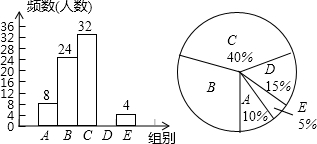
 网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:| 组别 | 学习时间x(h) | 频数(人数) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小时以上 | 4 |
分析 (1)根据A组的频数和百分比求出总人数,再利用D组的百分比求出n的值,n=总人数×D组的百分比;圆心角=百分比×360°;
(2)由(1)中n的值可得;
(3)先画树状图得出所有等可能的情况数,找到抽取的两名学生都来自九年级的情况数,计算概率即可.
解答 解:(1)8÷10%=80,n=15%×80=12,
∵总人数为80人,
扇形统计图中B组对应的圆心角为$\frac{24}{80}$×360°=108°,
故答案为:12,108;
(2)如下图: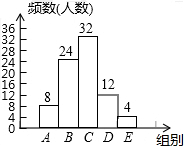
(3)画树状图为: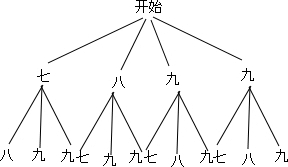
共12种可能,抽取的两名学生都来自九年级的有2种可能,
∴P(两个学生都是九年级)=$\frac{2}{12}$=$\frac{1}{6}$,
答:抽取的两名学生都来自九年级的概率为$\frac{1}{6}$.
点评 此题考查出利用画树状图法或列表法求概率,还考查了扇形统计图以及频数分布直方图;熟练掌握运算公式(①各部分扇形圆心角的度数=部分占总体的百分比×360°,②百分比=$\frac{该组频数}{数据总数}$)是解本题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
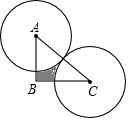 如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.
如图,在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,分别以$\frac{1}{2}$AC的长为半径作圆,将Rt△ABC截去两个扇形,则余下阴影部分的面积为( )cm2.| A. | $\frac{25}{4}$P | B. | 24-$\frac{5}{4}$P | C. | 24-$\frac{25}{6}$P | D. | 24-$\frac{25}{4}$P |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com