
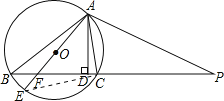
【题目】如图,△ABC内接于⊙O,AD是△ABC的高,⊙O的直径AE交BC于点F,点P在BC的延长线上,∠CAP=∠B。

(1)求证:PA是⊙O的切线;
(2)求证:PCPB=PDPF。
【答案】(1)、证明过程见解析;(2)、证明过程见解析.
【解析】
试题分析:(1)、连接EC,根据∠CAP=∠B得出∠E=∠B=∠CAP,根据直径得出∠ECA=90°,从而说明∠EAP=90°,得出答案;(2)、根据∠P=∠P,∠CAP=∠B得出△PAC∽△PBC,从而得到PA2=PBPC,根据∠P=∠P,∠ADP=∠FAP得出△ADP∽△FAP,从而说明AP2=DPPF,根据两个等式得出答案.
试题解析:(1)、连接EC,
∵∠CAP=∠B,
∴∠E=∠B=∠CAP,
∵⊙O的直径AE,
∴∠ECA=90°,
∴∠E+∠EAC=90°,
∴∠EAC+∠CAP=90°,
∴∠EAP=90°,
∴PA是⊙O的切线;
(2)、∵∠P=∠P,∠CAP=∠B,
∴△PAC∽△PBC,
∴![]() ,
,
∴PA2=PBPC,
∵∠P=∠P,∠ADP=∠FAP,
∴△ADP∽△FAP,
∴![]() ,
,
∴AP2=DPPF,
∴PCPB=PDPF.


科目:初中数学 来源: 题型:
【题目】某地气象统计资料表明,高度每增加1 000m,气温就降低大约6度. 现在地面的气温是35度,则10 000m高空的气温大约是 __________ 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是直线
是直线![]() 上的点,
上的点,![]() .
.
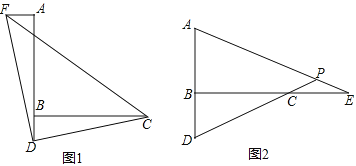
(1)如图1,过点![]() 作
作![]() ,并截取
,并截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,判断
,判断![]() 的形状并证明;
的形状并证明;
(2)如图2,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 以每秒
以每秒![]() 个单位长的速度,从点
个单位长的速度,从点![]() 出发沿
出发沿![]() 轴的正方向运动,
轴的正方向运动,![]() 是线段
是线段![]() 的中点.将线段
的中点.将线段![]() 以点
以点![]() 为中心,沿顺时针方向旋转
为中心,沿顺时针方向旋转![]() ,得到线段
,得到线段![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,运动时间为
,运动时间为![]() 秒.
秒.


(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)设![]() 的面积为
的面积为![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个城市来说,地铁开通意味着生活方式的改变.正在建设的成都地铁3号线双流境内全长约15.3千米,将极大地缩短双流和主城区成都的距离.日后,双流市民乘坐地铁,仅需25分钟就可直达市中心.用科学记数法表示15.3千米为( )米.
A. 15.3×103 B. 15.3×104 C. 1.53×103 D. 1.53×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决“最后一公里”的交通接驳问题,我市投放了大量公租自行车供市民使用.据统计,目前我市共有公租自行车3200辆.将3200用科学记数法表示应为( )
A. 0.32×104 B. 3.2×103 C. 3.2×102 D. 32×102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com