
【题目】如图,在边长为10的菱形ABCD中,对角线BD =16. 点E是AB的中点,P、Q是BD上的动点,且始终保持PQ =2, 则四边形AEPQ周长的最小值为_________.(结果保留根号)

【答案】7+![]()
【解析】
试题将菱形ABCD放置在平面直角坐标系中,使得B为原点,BD在x的正半轴上,根据题意得出A、B、E三点的坐标,将A平行向左移动2个单位到A'点,作A'关于x轴的对称点F,则F(6,-6),连EF,交x轴于点P,在x轴上向正方向上截取PQ=2,此时四边形AEPQ的周长最小,AQ+EP=A'P+EP=FP+EP=EF,由此即可得出结论.
试题解析:如图所示:
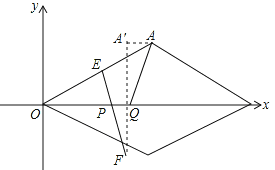
将菱形ABCD放置在平面直角坐标系中,使得B为原点,BD在x的正半轴上,
∵菱形ABCD的边长是10,对角线BD=16,点E是AB的中点,
∴A(8,6),B(0,0),E(4,3),将A平行向左移动2个单位到A'点,则A'(6,6),作A'关于x轴的对称点F,则F(6,-6),连EF,交x轴于点P,在x轴上向正方向上截取PQ=2,
此时,四边形AEPQ的周长最小,
∵AE=![]() =5,PQ=2,AQ+EP=A′P+EP=FP+EP=EF,
=5,PQ=2,AQ+EP=A′P+EP=FP+EP=EF,
∴四边形四边形AEPQ的周长=5+2+![]() =7+
=7+![]() .
.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某商场计划购进一批![]() 、
、![]() 两种空气净化装置,每台
两种空气净化装置,每台![]() 种设备价格比每台
种设备价格比每台![]() 种设备价格多0.7万元,花3万元购买
种设备价格多0.7万元,花3万元购买![]() 种设备和花7.2万元购买
种设备和花7.2万元购买![]() 种设备的数量相同.
种设备的数量相同.
(1)求![]() 种、
种、![]() 种设备每台各多少万元?
种设备每台各多少万元?
(2)根据销售情况,需购进![]() 、
、![]() 两种设备共20台,总费用不高于15万元,求
两种设备共20台,总费用不高于15万元,求![]() 种设备至少要购买多少台?
种设备至少要购买多少台?
(3)若每台![]() 种设备售价0.6万元,每台
种设备售价0.6万元,每台![]() 种设备售价1.4万元,在(2)的情况下商场应如何进货才能使这批空气净化装置售完后获利最多?
种设备售价1.4万元,在(2)的情况下商场应如何进货才能使这批空气净化装置售完后获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
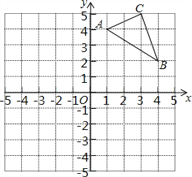
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出将△ABC向下平移5个单位后得到的△A1B1C1;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 经过点A(﹣3,0)和点B(2,0).直线
经过点A(﹣3,0)和点B(2,0).直线![]() (
(![]() 为常数,且
为常数,且![]() )与BC交于点D,与
)与BC交于点D,与![]() 轴交于点E,与AC交于点F.
轴交于点E,与AC交于点F.
(1)求抛物线的解析式;
(2)连接AE,求![]() 为何值时,△AEF的面积最大;
为何值时,△AEF的面积最大;
(3)已知一定点M(﹣2,0).问:是否存在这样的直线![]() ,使△BDM是等腰三角形?若存在,请求出
,使△BDM是等腰三角形?若存在,请求出![]() 的值和点D的坐标;若不存在,请说明理由.
的值和点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,

(1)试说明△ABC与△MED全等;
(2)若∠M=35°,求∠B的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com