
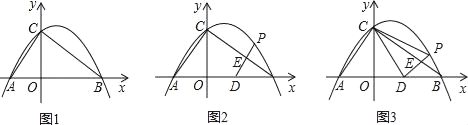
【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
【答案】(1)![]() (2)①(3,
(2)①(3,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() )②当m=
)②当m=![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为(![]() ,
,![]() ),S△CDP的最大值是
),S△CDP的最大值是![]()
【解析】试题(1)由Rt△ABC中,CO⊥AB可证△AOC∽△COB,由相似比得OC2=OAOB,设OA的长为x,则OB=5-x,代入可求OA,OB的长,确定A,B,C三点坐标,求抛物线解析式;
(2)根据△BDE为等腰三角形,分为DE=EB,EB=BD,DE=BD三种情况,分别求E点坐标;
(3)作辅助线,将求△CDP的面积问题转化.方法一:如图1,连接OP,根据S△CDP=S四边形CODP-S△COD=S△COP+S△ODP-S△COD,表示△CDP的面积;方法二:过点P作PE⊥x轴于点F,则S△CDP=S梯形COFP-S△COD-S△DFP,表示△CDP的面积;再利用二次函数的性质求出△CDP的最大面积和此时点P的坐标.
试题解析:
(1)设OA的长为x,则OB=5﹣x;
∵OC=2,AB=5,∠BOC=∠AOC=90°,∠OAC=∠OCB;
∴△AOC∽△COB,∴OC2=OAOB
∴22=x(5﹣x)
解得:x1=1,x2=4,
∵OA<OB,∴OA=1,OB=4;
∴点A、B、C的坐标分别是:A(﹣1,0),B(4,0),C(0,2);
方法一:设经过点A、B、C的抛物线的关系式为:y=ax2+bx+2,
将A、B、C三点的坐标代入得
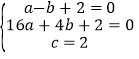 …
…
解得:a=![]() ,
,
所以这个二次函数的表达式为:y=![]()
方法二:设过点A、B、C的抛物线的关系式为:y=a(x+1)(x﹣4)…
将C点的坐标代入得:a=-![]()
所以这个二次函数的表达式为:y=![]()
(2)①当△BDE是等腰三角形时,点E的坐标分别是:(3,![]() ),(
),(![]() ,(4-
,(4-![]() ) .
) .
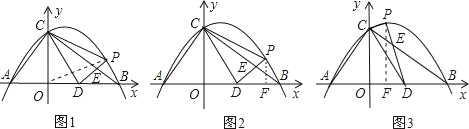
②如图1,连接OP,
S△CDP=S四边形CODP﹣S△COD=S△COP+S△ODP﹣S△COD
=
![]()
∴当m=![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为(![]() ,
,![]() ),
),
S△CDP的最大值是![]() .
.
另解:如图2、图3,过点P作PF⊥x轴于点F,则
S△CDP=S梯形COFP﹣S△COD﹣S△DFP
=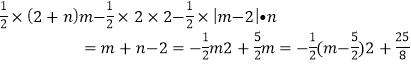
∴当m=![]() 时,△CDP的面积最大.此时P点的坐标为(
时,△CDP的面积最大.此时P点的坐标为(![]() ,
,![]() ),
),
S△CDP的最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况(如下图),进行整理后,绘制了如下两幅尚不完整的统计图:
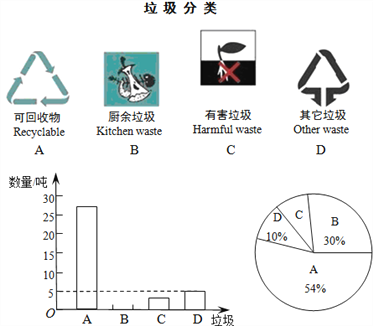
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,求出“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有 吨;
(4)调查发现,在可回收物中废纸垃圾约占![]() ,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
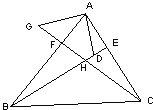
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按![]() 元
元![]() 计;B类收费标准如下:没有月租费,但通话费按
计;B类收费标准如下:没有月租费,但通话费按![]() 元
元![]() 计
计![]() 按照此类收费标准完成下列各题:
按照此类收费标准完成下列各题:
![]() 直接写出每月应缴费用
直接写出每月应缴费用![]() 元
元![]() 与通话时长
与通话时长![]() 分
分![]() 之间的关系式:
之间的关系式:
A类:______B类:______
![]() 若每月平均通话时长为300分钟,选择______类收费方式较少.
若每月平均通话时长为300分钟,选择______类收费方式较少.
![]() 求每月通话多长时间时,按
求每月通话多长时间时,按![]() 两类收费标准缴费,所缴话费相等.
两类收费标准缴费,所缴话费相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
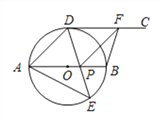
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
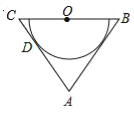
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB分别交坐标轴于A(2,0)、B(0,-6)两点直线上任意一点P(x,y),设点P到x轴和y轴的距离分别是m和n,则m+n的最小值为( )

A.2B.3C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
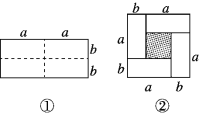
【题目】动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:_____________,_____________;
(2)请写出三个代数式(a+b)2,(a-b)2,ab之间的一个等量关系:___________________________;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=8,xy=7,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com