
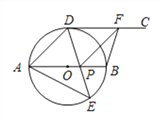
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
【答案】(1)证明见解析;(2)① 67.5°,②90°.
【解析】试题分析:(1)连接OD,根据切线的性质可得OD⊥CD,再由圆周角定理可得∠AOD=90°,即可得证;
(2)①根据菱形的性质和等腰三角形的性质求得∠ADP,在△ADE中利用三角形的内角和定理求得∠DAE的度数即可;
②判断四边形BFDP是正方形时,当DE是⊙O的直径即可求得∠DAE.
试题解析:(1)连接OD,∵射线DC切⊙O于点D,
∴OD⊥CD,
∵∠AED = 45°,
∴∠AOD = 2∠AED = 90°,
即∠ODF = ∠AOD ,
∴CD∥AB;
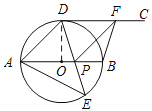
(2)①∵四边形ADFP是菱形,∴AD=AP,
∵在Rt△AOD中,OA=OD,∴∠DAO=45°,∴∠ADP=∠APD=(180°-45°)÷2=67.5°,
∴在△ADE中,∠DAE=180°-∠ADE-∠AED=180°-67.5°-45°=67.5°,
故答案为:67.5°;
②当BF⊥DF,DE⊥AB是四边形BFDP是正方形,
由题意可知,DE⊥AB时,DE经过⊙O的圆心,∴DE是⊙O的直径,∴∠DAE=90°,
故答案为:90°.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
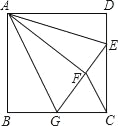
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=![]() .其中正确的是( )
.其中正确的是( )
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,从图中可以看出,终点表示的数是﹣2,已知A,B是数轴上的点.请参照图并思考,完成下列填空:
(1)如果点A表示数3,将点A向右移动7个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(2)如果点B表示数2,将点B向左移动9个单位长度,再向右移动5个单位长度,那么终点A表示的数是 ,A,B两点间的距离是 .

(3)如果点A表示的数是﹣4,将点A向右移动168个单位长度;再向左移动2个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是 ,A,B两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寻找公式,求代数式的值:从2开始,连续的的偶数相加,它们的和的情况如下表:

(1)根据上面的等式,你能发现当n个连续的的偶数相加时,它们的和S=2+4+6+8+……+2n= .
(2)并按照此规律计算:①2+4+6+……300的值;②162+164+166+……+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知从甲地到乙地,某船顺水航行需2小时,逆水航行需3小时,
(1)设轮船在静水中前进的速度是![]() 千米/时,水流的速度是y千米/时,则轮船共航行多少千米?
千米/时,水流的速度是y千米/时,则轮船共航行多少千米?
(2)如果轮船在静水中前进的速度是60千米/时,则水流的速度是多少千米/时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com