
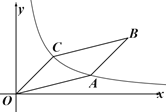
【题目】如图,![]() ABCO的面积为6,
ABCO的面积为6,![]() ,反比例函数
,反比例函数![]() 经过点A与点C,则k=_____.
经过点A与点C,则k=_____.
【答案】4
【解析】
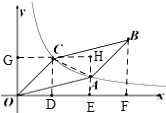
过C作CD⊥x轴于D,过A作AE⊥x轴于E,过B作BF⊥x轴于F,过C作CG⊥y轴于G,延长GC交EA延长线于H,连接AC,可得四边形OEHG是矩形,CH=DE,CG=OD,S△OCG=S△OCD,根据A、B坐标可得EF=2,根据平行四边形的性质可得OD=EF=2,由反比例函数![]() 经过点A与点C可得a=
经过点A与点C可得a=![]() ,C点坐标为(2,
,C点坐标为(2,![]() ),由平行四边形的面积可得S△OAC=3,根据S矩形OEHG=S△OCG+S△OAE+S△CAH+S△OAC列方程即可求出k值.
),由平行四边形的面积可得S△OAC=3,根据S矩形OEHG=S△OCG+S△OAE+S△CAH+S△OAC列方程即可求出k值.
如图,过C作CD⊥x轴于D,过A作AE⊥x轴于E,过B作BF⊥x轴于F,过C作CG⊥y轴于G,延长GC交EA延长线于H,连接AC,
∴四边形OEHC是矩形,
∴CH=DE,HE=OG,S△OCG=S△OCD
∵A(4,a),B(6,b),
∴EF=2,
∵OABC是平行四边形,
∴OD=EF=2,
∴CH=DE=OE-OD=2,
∵A、C在反比例函数y=![]() 上,
上,
∴a=![]() ,C(2,
,C(2,![]() ),
),
∴OG=HE=![]() ,
,
∴AH=HE-AE=![]() ,
,
∵S平行四边形OABC=6,
∴S△OAC=![]() S平行四边形OABC=3,
S平行四边形OABC=3,
∵反比例函数y=![]() 图象在第一象限,
图象在第一象限,
∴k>0,
∴S矩形OEHG=S△OCG+S△OAE+S△CAH+S△OAC=![]() k+
k+![]() k+
k+![]() ×
×![]() ×2+3=4×
×2+3=4×![]() ,
,
解得:k=4.
故答案为:4


科目:初中数学 来源: 题型:
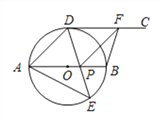
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE=_________时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE=_________时,四边形BFDP是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
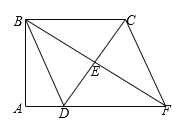
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分师生要去外地参加夏令营活动,车站提出两种车票价格优惠方案供学校选择:第一种方案是教师按原价付款,学生按原价的75%付款;第二种方案是师生都按原价的80%付款.已知该校有5名教师和x名学生参加此次夏令营活动,车票原价为100元/张.
(1)分别写出两种方案的购票款(列代数式并化简)
(2)如果两种方案的付款相同,那么参加夏令营的学生有多少人?
(3)当参加夏令营的学生人数为![]() 名时,试说明选择哪一种方案购票省钱?
名时,试说明选择哪一种方案购票省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何计算
(1)如图1,∠AOC,∠BOD都是直角,且∠AOB与∠AOD的度数比是2:11,求∠BOC的度数.
(2)如图2,点C分线段AB为3:4,AC<BC,点D分线段为AB上一点且11BD=3AD,若CD=10cm,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
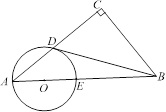
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
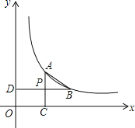
【题目】(1)如图,已知点A、B在双曲线![]() (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,点B的横坐标为b.A与B的坐标分别为_____、______(用b与k表示),由此可以猜想AP与CP的数量关系是______.
(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,点B的横坐标为b.A与B的坐标分别为_____、______(用b与k表示),由此可以猜想AP与CP的数量关系是______.
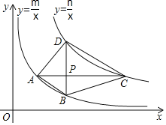
(2)四边形ABCD的四个顶点分别在反比例函数y![]() 与y
与y![]() 的图象上,对角线BD∥y轴,且BD⊥AC于点P,P是BD的中点,点B的横坐标为4.
的图象上,对角线BD∥y轴,且BD⊥AC于点P,P是BD的中点,点B的横坐标为4.
①当![]() 时,判断四边形ABCD的形状并说明理由.
时,判断四边形ABCD的形状并说明理由.
②四边形ABCD能否成为正方形?若能,直接写出此时m,n之间的数量关系;若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
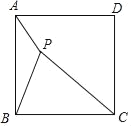
【题目】如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
(1)请画出旋转后的图形,说出此时△ABP以点B为旋转中心最少旋转了多少度;
(2)求出PG的长度;
(3)请你猜想△PGC的形状,并说明理由;
(4)请你计算∠BGC的角度.
查看答案和解析>>
科目:初中数学 来源: 题型:
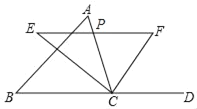
【题目】如图,△ABC中,点P是AC边上一个动点,过P作直线EF∥BC,交∠ACB的平分线于点E,交∠ACB的外角∠ACD平分线于点F.
(1)请说明:PE=PF;
(2)当点P在AC边上运动到何处时,四边形AECF是矩形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com