
【题目】如图,已知直线AB分别交坐标轴于A(2,0)、B(0,-6)两点直线上任意一点P(x,y),设点P到x轴和y轴的距离分别是m和n,则m+n的最小值为( )

A.2B.3C.5D.6
【答案】A
【解析】
先根据待定系数法求出直线AB的解析式,从而用含x的式子表示出m+n,分3种情况讨论:①x≥2,②0<x<2,③x≤0,算出最小值即可.
解:设直线AB的解析式为:y=kx+b
将A(2,0)、B(0,-6)代入得:
![]()
解得:![]()
∴直线AB的解析式为y=3x-6
∵P(x,y)是直线AB上任意一点
∴m=|3x-6|,n=|x|
∴m+n=|3x-6|+|x|
∴①当点P(x,y)满足x≥2时,m+n=4x-6≥2;
②当点P(x,y)满足0<x<2时,m+n=6-2x,此时2<m+n<6;
③当点P(x,y)满足x≤0时,m+n=6-4x≥6;
综上,m+n≥2
∴m+n的最小值为2
故选:A.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价280元,领带每条定价40元,在促销活动期间,该厂向客户提供了两种优惠方案(客户只能选择其中一种优惠方案):
方案一:买一套西装送一条领带;
方案二:西装按原价的9折收费,领带按原价的8折收费.
在促销活动期间,某客户要到该服装厂购买![]() 套西装,
套西装,![]() 条领带(
条领带(![]() ).
).
(1)该客户选择两种不同的方案所需费用分别是多少元?(用含![]() ,
,![]() 的式子表示并化简)
的式子表示并化简)
(2)若该客户需要购买10套西装,25条领带,则他选择哪种方案更划算?
(3)若该客户需要购买25套西装,35条领带,则他选择哪种方案更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
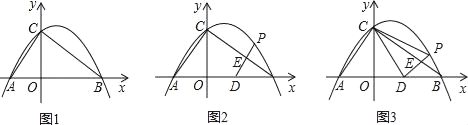
【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.

(1)求证:FD是⊙O的切线;
(2)若AF=8,tan∠BDF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
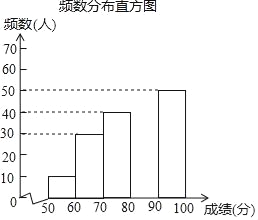
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
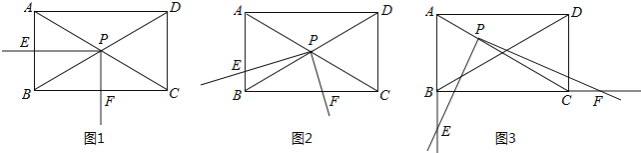
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
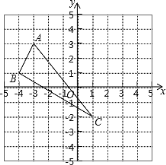
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿![]() 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿![]() 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的![]() (其中
(其中![]() 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);
(2)直接写出![]() 三点的坐标;
三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com