【题目】△ABC中，∠C=90°，内切圆与AB相切于点D，AD=2，BD=3，则△ABC的面积为（ ）
A.3B.6C.12D.无法确定
【答案】B
【解析】
易证得四边形OECF是正方形，然后由切线长定理可得AC=2+r，BC=3+r，AB=5，根据勾股定理列方程即可求得答案．
如图，设⊙O分别与边BC、CA相切于点E、F，
连接OE，OF，
∵⊙O分别与边AB、BC、CA相切于点D、E、F，
∴DE⊥BC，DF⊥AC，AF=AD=2，BE=BD=3，
∴∠OEC=∠OFC=90°，
∵∠C=90°，
∴四边形OECF是矩形，
∵OE=OF，
∴四边形OECF是正方形，
设EC=FC=r，
∴AC=AF+FC=2+r，BC=BE+EC=3+r，AB=AD+BD=2+3=5，
在Rt△ABC中，
=
+
，
∴
=
+
，
∴
，
即
解得：
或
（舍去）．
∴⊙O的半径r为1,
∴
．
故选：B
名师金手指领衔课时系列答案科目：初中数学 来源： 题型：
【题目】我们定义：如果圆的两条弦互相垂直，那么这两条弦互为“十字弦”，也把其中的一条弦叫做另一条弦的“十字弦”.如：如图，已知
的两条弦
，则
、
互为“十字弦”，是的“十字弦”，也是的“十字弦”.
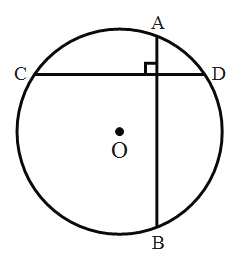
（1）若的半径为5，一条弦
，则弦的“十字弦”的最大值为______，最小值为______.
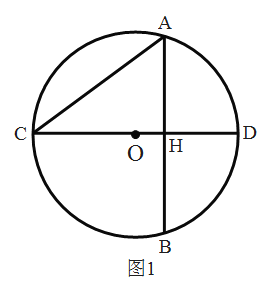
（2）如图1，若的弦恰好是的直径，弦与相交于
，连接
，若
，
，
，求证：、互为“十字弦”；
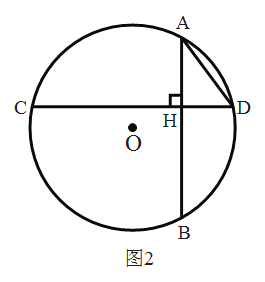
（3）如图2，若的半径为5，一条弦，弦是的“十字弦”，连接
，若
，求弦的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
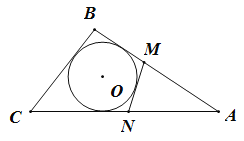
【题目】如图，△ABC周长为20cm，BC=6cm,圆O是△ABC的内切圆，圆O的切线MN与AB、CA相交于点M、N，则△AMN的周长为________cm.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中华人民共和国《城市道路路内停车泊位设置规范》规定：
一、在城市道路范围内，在不影响行人、车辆通行的情况下，政府有关部门可以规划停车泊位.停车泊位的排列方式有三种，如图所示：
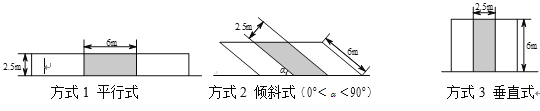
二、双向通行道路，路幅宽
米以上的，可在两侧设停车泊位，路幅宽
米到米的，可在单侧设停车泊位，路幅宽米以下的，不能设停车泊位；
三、规定小型停车泊位，车位长
米，车位宽
米；
四、设置城市道路路内机动车停车泊位后，用于单向通行的道路宽度应不小于
米.
根据上述的规定，在不考虑车位间隔线和车道间隔线的宽度的情况下，如果在一条路幅宽为
米的双向通行车道设置同一种排列方式的小型停车泊位，请回答下列问题：
（1）可在该道路两侧设置停车泊位的排列方式为 ；
（2）如果这段道路长
米，那么在道路两侧最多可以设置停车泊位 个.
(参考数据：
，
)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某软件开发公司开发了A、B两种软件，每种软件成本均为1400元，售价分别为2000元、1800元，这两种软件每天的销售额共为112000元，总利润为28000元．
（1）该店每天销售这两种软件共多少个？
（2）根据市场行情，公司拟对A种软件降价销售，同时提高B种软件价格．此时发现，A种软件每降50元可多卖1件，B种软件每提高50元就少卖1件．如果这两种软件每天销售总件数不变，那么这两种软件一天的总利润最多是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
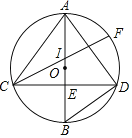
【题目】如图，⊙O中直径AB⊥弦CD于E，点F是
的中点，CF交AB于I，连接BD、AC、AD．
（1）求证：BI＝BD；
（2）若OI＝1，OE＝2，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司从2016年开始投入技术改进资金，经技术改进后，其产品的成本不断降低，具体数据如下表：
年度 | 投入技改资金x/万元 | 产品成本y/(万元/件) |
2016 | 2 | 18 |
2017 | 3 | 12 |
2018 | 4 | 9 |
2019 | 4.5 | 8 |
（1）根据表格中数据，求y关于x的函数解析式。
（2）在图中的网格中建立适当的平面直角坐标系，画出该函数的大致图像。
（3）如果打算在2020年让产品成本不高于7万元，则投入技改资金至少为 万元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
