
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
![]() 当
当![]() 取何值时,此方程有两个不相等的实数根;
取何值时,此方程有两个不相等的实数根;
![]() 当抛物线
当抛物线![]() 与轴两个交点的横坐标均为整数,且
与轴两个交点的横坐标均为整数,且![]() 为正整数时,求此抛物线的解析式.
为正整数时,求此抛物线的解析式.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=kx+b交抛物线y=![]() 于点A、B(A在B点左侧),过点B的直线BD与抛物线只有唯一公共点,且与y轴负半轴交于点D.
于点A、B(A在B点左侧),过点B的直线BD与抛物线只有唯一公共点,且与y轴负半轴交于点D.
(1)若k=![]() ,b=2,求点A、B两点坐标;
,b=2,求点A、B两点坐标;
(2)AB交y轴于点C,若BC=CD,OC=CE,点E在y轴正半轴上,EF∥x轴,交抛物线于点F,求EF的长;
(3)在(1)的条件下,P为射线BD上一动点,PN∥y轴交抛物线于点N,交直线于点Q,PM∥AN交直线于点M,求MQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
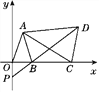
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别以
分别以![]() 、
、![]() 的速度从点
的速度从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 向点
向点![]() 移动.
移动.

![]() 若点
若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 随点
随点![]() 的停止而停止移动,点
的停止而停止移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过多长时间
同时出发,问经过多长时间![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ?
?
![]() 若点
若点![]() 沿着
沿着![]() 移动,点
移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 移动到点
移动到点![]() 停止时,点
停止时,点![]() 随点
随点![]() 的停止而停止移动,试探求经过多长时间
的停止而停止移动,试探求经过多长时间![]() 的面积为
的面积为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
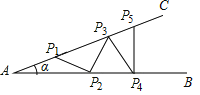
【题目】如图钢架中,∠A=![]() ,焊上等长的钢条P1P2, P2P3, P3P4, P4P5……来加固钢架.著P1A= P1P2,且恰好用了4根钢条,则α的取值范圈是( )
,焊上等长的钢条P1P2, P2P3, P3P4, P4P5……来加固钢架.著P1A= P1P2,且恰好用了4根钢条,则α的取值范圈是( )
A.15°≤ a <18°
B.15°< a ≤18°
C.18°≤ a <22.5°
D.18° < a ≤ 22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下文字并解决问题:对于形如![]() 这样的二次三项式,我们可以直接用公式法把它分解成
这样的二次三项式,我们可以直接用公式法把它分解成![]() 的形式,但对于二次三项式
的形式,但对于二次三项式![]() ,就不能直接用公式法分解了.此时,我们可以在
,就不能直接用公式法分解了.此时,我们可以在![]() 中间先加上一项
中间先加上一项![]() ,使它与
,使它与![]() 的和构成一个完全平方式,然后再减去
的和构成一个完全平方式,然后再减去![]() ,则整个多项式的值不变.即:
,则整个多项式的值不变.即: ,像这样,把一个二次三项式变成含有完全平方式的形式的方法,叫做配方法.
,像这样,把一个二次三项式变成含有完全平方式的形式的方法,叫做配方法.
![]() 利用“配方法”因式分解:
利用“配方法”因式分解:![]()
![]() 如果
如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com