
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
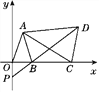
【答案】(1)证明见解析(2)证明见解析(3)点P在y轴上的位置不发生改变
【解析】试题分析:(1)先根据非负数的性质求出a、b的值,作AE⊥OB于点E,由SAS定理得出△AEO≌△AEB,根据全等三角形的性质即可得出结论;
(2)先根据∠CAD=∠OAB,得出∠OAC=∠BAD,再由SAS定理即可得出△AEO≌△AEB;
(3)设∠AOB=∠ABO=α,由全等三角形的性质可得出∠ABD=∠AOB=α,故∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,再由OB=2,∠POB=90°可知OP的长度不变,故可得出结论.
试题解析:
(1)证明:∵|a+b-3|+(a-2b)2=0,
∴![]()
解得![]()
∴A(1,3),B(2,0).
作AE⊥OB于点E,
∵A(1,3),B(2,0),
∴OE=1,BE=2-1=1,
在△AEO与△AEB中,
∵
∴△AEO≌△AEB,
∴OA=AB.
(2)证明:∵∠CAD=∠OAB,
∴∠CAD+∠BAC=∠OAB+∠BAC,
即∠OAC=∠BAD.在△AOC与△ABD中,
∵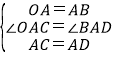
∴△AOC≌△ABD.
(3)点P在y轴上的位置不发生改变.理由:
设∠AOB=α.∵OA=AB,
∴∠AOB=∠ABO=α.
由(2)知,△AOC≌△ABD,
∴∠ABD=∠AOB=α.
∵OB=2,∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,∠POB=90°,
易知△POB形状、大小确定,
∴OP长度不变,
∴点P在y轴上的位置不发生改变.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=![]() (x>0)上,且AB=
(x>0)上,且AB=![]() ,求k的值;
,求k的值;
(3)若a=![]() ,b=
,b=![]() ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校创造节插花艺术比赛中同学们制作了若干个甲、乙、丙三种造型的花篮.甲种花篮由9朵玫瑰花、16朵水仙花和10朵百合花搭配而成,乙种花篮由6朵玫瑰花、8朵水仙花搭配而成.丙种花篮由6朵玫瑰花、12朵水仙花和10朵百合搭配而成.这些花篮一共用了240朵玫瑰花,300朵百合花,则水仙花一共用了_____朵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 与
与![]() 关于坐标原点对称,那么点
关于坐标原点对称,那么点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 后的对应点
后的对应点![]() 的坐标是( )
的坐标是( )
A. (-1,2) B. (1,-2) C. (-1,-2) D. (1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店用1050元购进第一批某种钢笔,很快卖完,又用1440元购进第二批该种钢笔,但第二批每支钢笔的进价是第一批进价的1.2倍,数量比第一批多了10支。
(1)求第一批每支钢笔的进价是多少元?
(2)第二批钢笔按24元/支的价格销售,销售一定数量后,根据市场情况,商店决定对剩余的钢笔全按8折一次性打折销售,但要求第二批钢笔的利润率不低于20%,问至少销售多少支后开始打折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.

请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )

A. 前2分钟,乙的平均速度比甲快
B. 5分钟时两人都跑了500米
C. 甲跑完800米的平均速度为100米/分
D. 甲乙两人8分钟各跑了800米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,延长AB到点E,连接EC,使得∠BCE=∠BAC
(1)求证:EC是⊙O的切线;
(2)过点A作AD⊥EC的延长线于点D,若AD=5,DE=12,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com