
【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=![]() (x>0)上,且AB=
(x>0)上,且AB=![]() ,求k的值;
,求k的值;
(3)若a=![]() ,b=
,b=![]() ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.

【答案】(1)C(0,1),D(2,1);(2)k=2;(3)y=﹣x+![]() .
.
【解析】
(1)如图1中,设C(m,n),D(p,q).利用中点坐标公式计算即可;
(2)如图2中,由题意点C的纵坐标为2,点D的横坐标为2,由点C、D在反比例函数y=![]() 上,可以假设C(m,2),D(2,m),根据AB=CD=
上,可以假设C(m,2),D(2,m),根据AB=CD=![]() ,2-m=1,可得m=1,求出点D坐标即可解决问题;
,2-m=1,可得m=1,求出点D坐标即可解决问题;
(3)设C(m,n),D(p,q).利用中点坐标公式求出C、D两点坐标,再利用待定系数法即可解决问题;
解:(1)如图1中,设C(m,n),D(p,q).

由题意A(2,0),B(0,1),
∵A、C关于M对称,B、D关于M对称,
∴![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,
解得m=0,n=2,p=2,q=1,
∴C(0,1),D(2,1).
(2)如图2中,由题意点C的纵坐标为2,点D的横坐标为2,

∵点C、D在反比例函数y=![]() 上,
上,
∴可以假设C(m,2),D(2,m),
∵AB=CD=![]() ,
,
∴2﹣m=1,
∴m=1,
∴C(1,2),D(2,1),
把C(1,2)代入y=![]() 中,得到k=2.
中,得到k=2.
(3)设C(m,n),D(p,q).由题意A(![]() ,0),B(0,
,0),B(0,![]() ),
),
∵A、C关于M对称,B、D关于M对称,
∴![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,
解得m=![]() ,n=2,p=2,q=
,n=2,p=2,q=![]() ,
,
∴C(![]() ,2),D(2,
,2),D(2,![]() ),设直线CD的解析式为y=kx+b,
),设直线CD的解析式为y=kx+b,
则有 ,解得
,解得 ,
,
∴直线CD的解析式为y=﹣x+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠ABC的大小是( )
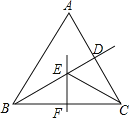
A.32°B.56°C.64°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=kx+b交抛物线y=![]() 于点A、B(A在B点左侧),过点B的直线BD与抛物线只有唯一公共点,且与y轴负半轴交于点D.
于点A、B(A在B点左侧),过点B的直线BD与抛物线只有唯一公共点,且与y轴负半轴交于点D.
(1)若k=![]() ,b=2,求点A、B两点坐标;
,b=2,求点A、B两点坐标;
(2)AB交y轴于点C,若BC=CD,OC=CE,点E在y轴正半轴上,EF∥x轴,交抛物线于点F,求EF的长;
(3)在(1)的条件下,P为射线BD上一动点,PN∥y轴交抛物线于点N,交直线于点Q,PM∥AN交直线于点M,求MQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:(一)如果我们能找到两个实数x、y使![]() 且
且![]() ,这样
,这样![]() ,那么我们就称
,那么我们就称![]() 为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
例如:![]() .
.
(二)在进行二次根式的化简与运算时,我们有时还会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: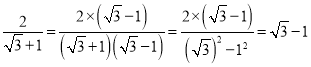 ,那么我们称这个过程为分式的分母有理化.
,那么我们称这个过程为分式的分母有理化.
根据阅读材料解决下列问题:
(1)化简“和谐二次根式”:①![]() ___________,②___________;
___________,②___________;
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的小数部分为
的小数部分为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(-3x2y)3·(-2xy3);
(2)-x(-x-y)
(3)-5x(-x2+2x+1 )
(4)(3x+y)(-y+3x)
(5)2a(a-2a3)-(-3a2)2;
(6)(x-3)(x+2)-(x+1)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
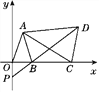
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com