
【题目】已知点![]() 与
与![]() 关于坐标原点对称,那么点
关于坐标原点对称,那么点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 后的对应点
后的对应点![]() 的坐标是( )
的坐标是( )
A. (-1,2) B. (1,-2) C. (-1,-2) D. (1,2)
【答案】C
【解析】
首先得出P点坐标,再根据题意画出P的对称点P′,过P′作P′N⊥y轴于N,过P作PM⊥x轴于M,得出△POM≌△P′ON,推出P′N=PM,ON=OM,根据P的坐标即可求出答案.
∵点A(a,1)与B(﹣2,b)关于坐标原点对称,∴a=2,b=﹣1,∴P点坐标为:(2,﹣1),以直角坐标系原点为中心,将点P(2,﹣1)顺时针旋转90°后到P′点,过P′作P′N⊥y轴于N,过P作PM⊥x轴于M,则OP=OP′,∠P′OP=90°,∠P′NO=∠PMO=90°,∴∠MOP=∠NO P′.在△P′ON和△POM中,∵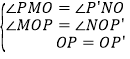 ,∴△POM≌△P′ON(AAS),∴P′N=PM,ON=OM.
,∴△POM≌△P′ON(AAS),∴P′N=PM,ON=OM.
∵P(2,﹣1),∴OM=2,PM=1,∴P′(﹣1,﹣2).
故选C.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(-3x2y)3·(-2xy3);
(2)-x(-x-y)
(3)-5x(-x2+2x+1 )
(4)(3x+y)(-y+3x)
(5)2a(a-2a3)-(-3a2)2;
(6)(x-3)(x+2)-(x+1)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
(1)若∠ABC=50°,∠ACB=80°,则∠A= 度,∠P= 度
(2)∠A与∠P的数量关系为 ,并说明理由.
(应用)如图②,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.∠ABC的外角平分线与∠ACB的外角平分线相交于点Q.直接写出∠A与∠Q的数量关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
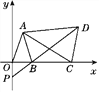
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
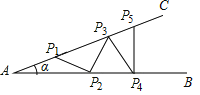
【题目】如图钢架中,∠A=![]() ,焊上等长的钢条P1P2, P2P3, P3P4, P4P5……来加固钢架.著P1A= P1P2,且恰好用了4根钢条,则α的取值范圈是( )
,焊上等长的钢条P1P2, P2P3, P3P4, P4P5……来加固钢架.著P1A= P1P2,且恰好用了4根钢条,则α的取值范圈是( )
A.15°≤ a <18°
B.15°< a ≤18°
C.18°≤ a <22.5°
D.18° < a ≤ 22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com