
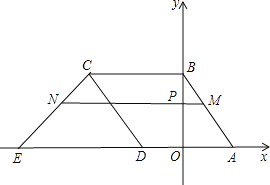
ĄŸÌâÄżĄżÖ±Ïß![]() ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăBŁŹÁâĐÎABCDÈçÍŒ·ĆÖĂÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÆäÖĐ”ăDÔÚxÖážș°ëÖáÉÏŁŹÖ±Ïßy=x+mŸčę”ăCŁŹœ»xÖáÓÚ”ăEŁź
ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăBŁŹÁâĐÎABCDÈçÍŒ·ĆÖĂÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÆäÖĐ”ăDÔÚxÖážș°ëÖáÉÏŁŹÖ±Ïßy=x+mŸčę”ăCŁŹœ»xÖáÓÚ”ăEŁź
ąÙÇëÖ±œÓĐŽłö”ăCĄą”ăD”ÄŚű±êŁŹČąÇółöm”ÄÖ”Ł»
ąÚ”ăPŁš0ŁŹtŁ©ÊÇÏ߶ÎOBÉÏ”ÄÒ»žö¶Ż”㣚”ăPČ»ÓëOĄąBÖŰșÏŁ©ŁŹŸčę”ăPÇÒÆœĐĐÓÚxÖá”ÄÖ±Ïßœ»ABÓÚMĄąœ»CEÓÚNŁźÉèÏ߶ÎMN”Äł€¶ÈÎȘdŁŹÇódÓëtÖźŒä”ÄșŻÊęčŰϔʜŁšČ»ÒȘÇóĐŽŚÔ±äÁż”ÄÈĄÖ”·¶Î§Ł©Ł»
ąÛ”ăPŁš0ŁŹtŁ©ÊÇyÖáŐę°ëÖáÉÏ”ÄÒ»žö¶Ż”㣏ÎȘșÎ֔ʱ”ăPĄąCĄąDÇĄșĂÄÜŚéłÉÒ»žö”ÈŃüÈęœÇĐÎŁż
ĄŸŽđ°žĄżŁš1Ł©m=9Ł»Łš2Ł©![]() Ł»Łš3Ł©t=4ŁŹ»òt=
Ł»Łš3Ł©t=4ŁŹ»òt=![]() ŁŹt=
ŁŹt=![]() ʱŁŹĄśPCDŸùÎȘ”ÈŃüÈęœÇĐÎ.
ʱŁŹĄśPCDŸùÎȘ”ÈŃüÈęœÇĐÎ.
ĄŸœâÎöĄż
ÊÔÌ⣚1Ł©ÓÉÖ±ÏߔĜâÎöÊœżÉÇółöAșÍB”ă”ÄŚű±êŁŹÔÙžùŸĘÁâĐΔÄĐÔÖÊŒŽżÉÇółö”ăCĄą”ăD”ÄŚű±êŁŹ°Ń”ăC”ÄŚű±êŽúÈëÖ±Ïßy=x+mŒŽżÉÇółöm”ÄÖ”Ł»
Łš2Ł©Éè”ăM”ÄŚű±êÎȘŁšxMŁŹtŁ©ŁŹ”ăN”ÄŚű±êÎȘŁšxNŁŹtŁ©ŁŹÊŚÏÈÇółöxM=©![]() t+3ŁŹÔÙÇółöxN=t©9ŁŹœű¶ű”Ă”œd=xM©xN=©
t+3ŁŹÔÙÇółöxN=t©9ŁŹœű¶ű”Ă”œd=xM©xN=©![]() t+3©Łšt©9Ł©=©
t+3©Łšt©9Ł©=©![]() t+12Ł»
t+12Ł»
Łš3Ł©ÓÉAșÍB”ÄŚű±êżÉÇółöAB”Äł€ŁŹÔÙ·ÖÈęÖÖÇéżö·Ö±đÌÖÂÛÇółö·ûșÏÌâÒâ”ÄtÖ”ŒŽżÉŁź
ÊÔÌâœâÎöŁșŁš1Ł©ĄßÖ±Ïßy=©![]() x+4ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăBŁŹ
x+4ÓëxÖ᜻ÓÚ”ăAŁŹÓëyÖ᜻ÓÚ”ăBŁŹ
Ąà”ăA”ÄŚű±êÎȘŁš3ŁŹ0Ł©”ăB”ÄŚű±êÎȘŁš0ŁŹ4Ł©ŁŹ
ĄßËıßĐÎABCDÊÇÁâĐÎŁŹ
Ąà”ăC”ÄŚű±êÎȘŁš©5ŁŹ4Ł©ŁŹ”ăD”ÄŚű±êÎȘŁš©2ŁŹ0Ł©ŁŹ
ĄßÖ±Ïßy=x+mŸčę”ăCŁŹ
Ąàm=9ŁŹ
Łš2Ł©ĄßMN Ÿčę”ăPŁš0ŁŹtŁ©ÇÒÆœĐĐÓÚxÖᣏ
ĄàżÉÉè”ăM”ÄŚű±êÎȘŁšxMŁŹtŁ©ŁŹ”ăN”ÄŚű±êÎȘŁšxNŁŹtŁ©ŁŹ
Ąß”ăMÔÚÖ±ÏßABÉÏŁŹ
Ö±ÏßAB”ÄœâÎöÊœÎȘy=©![]() x+4ŁŹ
x+4ŁŹ
Ąàt=![]() ŁŹ”ĂxM=©
ŁŹ”ĂxM=©![]() t+3ŁŹ
t+3ŁŹ
ÍŹÀí”ăNÔÚÖ±ÏßCEÉÏŁŹÖ±ÏßCE”ÄœâÎöÊœÎȘy=x+9ŁŹ
Ąàt=xN+9ŁŹ”ĂxN=t©9ŁŹ
ĄßMNĄÎxÖáÇÒÏ߶ÎMN”Äł€¶ÈÎȘdŁŹ
Ąàd=xM©xN=©![]() t+3©Łšt©9Ł©=©
t+3©Łšt©9Ł©=©![]() t+12Ł»
t+12Ł»
Łš3Ł©ĄßÖ±ÏßAB”ÄœâÎöÊœÎȘy=©![]() x+4ŁŹ
x+4ŁŹ
Ąà”ăA ”ÄŚű±êÎȘŁš3ŁŹ0Ł©ŁŹ”ăB”ÄŚű±êÎȘŁš0ŁŹ4Ł©ŁŹAB=5ŁŹ
ĄßËıßĐÎABCDÊÇÁâĐÎŁŹ
ĄàAB=BC=CD=5ŁŹ
Ąà”ăPÔ˶Ż”œ”ăBʱŁŹĄśPCDŒŽÎȘĄśBCDÊÇÒ»žö”ÈŃüÈęœÇĐÎŁŹŽËʱ=4Ł»
Ąß”ăPŁš0ŁŹtŁ©ÊÇyÖáŐę°ëÖáÉÏ”ÄÒ»žö¶Ż”㣏
ĄàOP=tŁŹPB=|t©4|ŁŹ
Ąß”ăD”ÄŚű±êÎȘŁš©2ŁŹ0Ł©ŁŹ
ĄàOD=2ŁŹÓÉčŽčɶšÀí”ĂPD2=OD2+OP2=4+t2ŁŹ
ÍŹÀíŁŹCP2=BC2+BP2=25+Łšt©4Ł©2ŁŹ
”±PD=CD=5ʱŁŹPD2=4+t2=25ŁŹ
Ąàt=![]() ŁšÉážșŁ©ŁŹ
ŁšÉážșŁ©ŁŹ
”±PD=CPʱŁŹPD2=CP2ŁŹ4+t2=25+Łšt©4Ł©2ŁŹ
Ąàt=![]() ŁŹ
ŁŹ
ŚÛÉÏËùÊöŁŹt=4ŁŹ»òt=![]() ŁŹt=
ŁŹt=![]() ʱŁŹĄśPCDŸùÎȘ”ÈŃüÈęœÇĐÎŁź
ʱŁŹĄśPCDŸùÎȘ”ÈŃüÈęœÇĐÎŁź


 ÔĶÁżìł”Ï”ÁĐŽđ°ž
ÔĶÁżìł”Ï”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
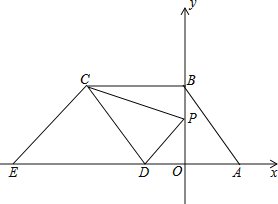
ĄŸÌâÄżĄżÎíöČÌìÆűŃÏÖŰÓ°ÏìÊĐĂń”ÄÉú»îÖÊÁżĄŁÔÚœńÄêșźŒÙÆÚŒäŁŹÄłĐŁŸĆÄꌶһ°à”ÄŚÛșÏÊ”ŒùĐĄŚéѧÉú¶ÔĄ°ÎíöČÌìÆű”ÄÖśÒȘłÉÒòĄ±Ëæ»ú”śČéÁËËùÔÚłÇÊĐČż·ÖÊĐĂńŁŹČą¶Ô”śČéœáčûœűĐĐÁËŐûÀíŁŹ»æÖÆÁËÏÂÍŒËùÊŸ”ÄČ»ÍêŐû”ÄÍłŒÆÍŒ±íŁș
Śé±đ | ÎíöČÌìÆű”ÄÖśÒȘłÉÒò | °Ù·Ö±È |
A | č€Ò”ÎÛÈŸ | 45% |
B | Æûł”ÎČÆűĆĆ·Ć |
|
C | ÂŻŃÌÆűĆĆ·Ć | 15% |
D | ÆäËûŁšÀÄżłÀÄ·„”ÈŁ© |
|
ÇëžùŸĘÍłŒÆÍŒ±í»ŰŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©±ŸŽÎ±»”śČé”ÄÊĐĂńčČÓжàÉÙÈËŁżČąÇó![]() șÍ
șÍ![]() ”ÄÖ”Ł»
”ÄÖ”Ł»
Łš2Ł©ÇëČčÈ«ÌőĐÎÍłŒÆÍŒŁŹČąŒÆËăÉÈĐÎÍłŒÆÍŒÖĐÉÈĐÎÇűÓò![]() Ëù¶ÔÓŠ”ÄÔČĐĜǔĶÈÊꣻ
Ëù¶ÔÓŠ”ÄÔČĐĜǔĶÈÊꣻ
Łš3Ł©ÈôžĂÊĐÓĐ100ÍòÈËżÚŁŹÇëčÀŒÆÊĐĂńÈÏÎȘĄ°č€Ò”ÎÛÈŸșÍÆûł”ÎČÆűĆĆ·ĆÊÇÎíöČÌìÆűÖśÒȘłÉÒòĄ±”ÄÈËÊę.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŁš±ŸÌâÂú·Ö7·ÖŁ©ÒŃÖȘčŰÓÚx”Ä·œłÌ![]() ÓĐÁœžöČ»Ïà”È”ÄÊ”ÊęžùŁź
ÓĐÁœžöČ»Ïà”È”ÄÊ”ÊęžùŁź
Łš1Ł©Çók”ÄÈĄÖ”·¶Î§Ł»
Łš2Ł©ÊÇ·ńŽæÔÚÊ”ÊękŁŹÊčŽË·œłÌ”ÄÁœžöÊ”Êęžù”Ä”čÊęșÍ”ÈÓÚ0ŁżÈôŽæÔÚŁŹÇółök”ÄÖ”Ł»ÈôČ»ŽæÔÚŁŹË”ĂśÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
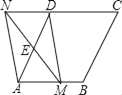
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÁâĐÎABCDÖĐŁŹABŁœ4ŁŹĄÏDABŁœ60ĄăŁŹ”ăEÊÇAD±ß”ÄÖД㣏”ăMÊÇAB±ßÉÏ”ÄÒ»žö¶Ż”㣚ȻÓë”ăAÖŰșÏŁ©ŁŹŃÓł€MEœ»CD”ÄŃÓł€ÏßÓÚ”ăNŁŹÁŹœÓMDŁŹANŁź
Łš1Ł©ÇóÖ€ŁșËıßĐÎAMDNÊÇÆœĐĐËıßĐÎŁ»
Łš2Ł©”±AM”ÄÖ”ÎȘĄĄ ĄĄÊ±ŁŹËıßĐÎAMDNÊÇŸŰĐÎŁŹÇëÄă°ŃČÂÏëłö”ÄAMÖ”ŚśÎȘÒŃÖȘÌőŒțŁŹË”ĂśËıßĐÎAMDNÊÇŸŰĐΔÄÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚŸŰĐÎABCDÖĐ ŁŹAB=8 , BC=6, ”ăPÔÚ±ßABÉÏĄŁÈôœ«ĄśDAPŃŰDPŐÛ”ț ŁŹÊč”ăAÂäÔÚŸŰĐζԜÇÏßÉϔĔăAŁŹŽŠŁŹÔòAP”Äł€ÎȘ__________ĄŁ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŒŚĄąÒÒÁœł”·Ö±đŽÓAĄąBÁœ”ŰÍŹÊ±łö·ąŁŹŃŰÍŹÒ»Ìőč«Â·ÏàÏò¶űĐĐŁŹÏàÓöʱŒŚĄąÒÒËùŚß·łÌ”ıÈÎȘ2Łș3ŁŹŒŚĄąÒÒÁœł”ÀëABÖĐ”ăC·łÌyŁšÇ§ĂŚŁ©ÓëŒŚł”łö·ąÊ±ŒätŁšĐĄÊ±Ł©”ÄčŰϔ͌ÏóÈçÍŒËùÊŸŁŹÔòÏÂÁĐË”·šŁșąÙAĄąBÁœ”ŰÖźŒä”ÄŸàÀëÎȘ180ǧÌŁ»ąÚÒÒł””ÄËÙ¶ÈÎȘ36ǧÌ/ĐĄÊ±Ł»ąÛa=3.75Ł»ąÜ”±ÒÒł””œŽïÖŐ”ăʱŁŹŒŚł”ŸàÀëÖŐ”ă»čÓĐ30ǧÌŁźÆäÖĐŐęÈ·”ÄœáÂÛÓĐŁšĄĄĄĄŁ©
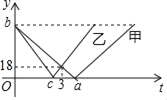
A. 1žö B. 2žö C. 3žö D. 4žö
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒ»Ìő”ŰÏÂčÜÏßÓÉŒŚč€łÌ¶Ó”„¶ÀÆÌÉèĐèÒȘ12ÌìŁŹÓÉÒÒč€łÌ¶Ó”„¶ÀÆÌÉèĐèÒȘ24ÌìŁŹÒŃÖȘŒŚč€łÌ¶ÓÆÌÉèĂżÌìĐèÖ§ž¶č€łÌ·Ń2000ÔȘŁŹÒÒč€łÌ¶ÓÆÌÉèĂżÌìĐèÖ§ž¶č€łÌ·Ń1500ÔȘ.
Łš1Ł©ŒŚĄąÒÒÁœ¶ÓșÏŚśÊ©č€¶àÉÙÌìÄÜÍêłÉžĂčÜÏß”ÄÆÌÉèŁż
Łš2Ł©ÓÉÁœ¶ÓșÏŚśÍêłÉžĂčÜÏßÆÌÉè耳ÌčČĐèÖ§ž¶č€łÌ·Ń¶àÉÙÔȘŁż
Łš3Ł©žùŸĘÊ”ŒÊÇéżöŁŹÈôžĂ耳ÌÒȘÇó10ÌìÍêłÉŁŹŽÓœÚÔŒŚÊœđ”ĜǶÈÓŠÔőŃù°ČĆĆÊ©č€Łż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÀîÜ͏ѧÔçÉÏÆïŚÔĐĐł”ÉÏѧŁŹÖĐÍŸÒò”À·ʩč€ĐèČœĐĐÒ»¶Î·ŁŹ”œŃ§ĐŁčČÓĂʱ18·ÖÖÓ,ËûÆïŚÔĐĐł””ÄÆœŸùËÙ¶ÈÊÇ300ĂŚ/·ÖÖÓŁŹČœĐĐ”ÄÆœŸùËÙ¶ÈÊÇ120ĂŚ/·ÖÖÓŁŹËûŒÒÀëѧУ”ÄŸàÀëÊÇ4500ĂŚ.
Łš1Ł©ÀîĂśÉÏŃ§Ê±ÆïŚÔĐĐł””Ä·łÌșÍČœĐДķłÌ·Ö±đÎȘ¶àÉÙĂŚŁż
Łš2Ł©·ĆѧșóÀîĂśŽÓ17:40żȘÊŒÀëĐŁ»ŰŒÒŁŹ”«ŽËʱ”ÀÂ·Ê©č€”Ä”Ű¶ÎÔöł€ÁË600ĂŚŁŹÈçčû°ŽŐŐÉÏŃ§Ê±”ÄËÙ¶ÈŁŹÎÊÀîĂśÄÜ·ńÔÚ18:00֟ǰ”œŒÒŁżÇëÍščęŒÆËă˔Ü.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŐę·œĐÎA1B1C1OŁŹA2B2C2C1ŁŹA3B3C3C2ŁŹĄ°ŽÈçÍŒ”Ä·œÊœ·ĆÖĂŁŹ”ăA1ŁŹA2ŁŹA3ĄșÍ”ăC1ŁŹC2ŁŹC3Ą·Ö±đÔÚÖ±Ïßy=x+1șÍxÖáÉÏŁŹÔò”ăBn”ÄŚű±êÎȘ_____Łź

Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com