
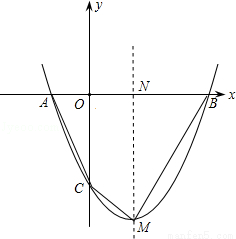
已知抛物线与y轴交于点C,与x轴交于A( ,0),B(
,0),B( ,0),(
,0),( <
< )两点,顶点M的纵坐标为
)两点,顶点M的纵坐标为 ,若
,若 ,
, 是方程
是方程 的两根,且
的两根,且 。
。
(1)、求A、B两点的坐标。
(2)、求抛物线的表达式及点C的坐标。
(3)、抛物线上是否存在点P,使△PAB的面积等于四边形ACMB面积的2倍,若存在,求出点P的坐标,若不存在,请说明理由。
(1)A(﹣1,0),B(3,0);(2)y=x2﹣2x﹣3;C(0,-3);(3)存在符合条件的P点,且坐标为(1﹣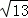 ,9),(1+
,9),(1+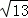 ,9)
,9)
【解析】
试题分析:(1)根据韦达定理可得出A、B两点横坐标的和与积,联立x12+x22=10,可求出m的值,进而可求出A、B的坐标.
(2)根据A、B的坐标,可得出抛物线的对称轴的解析式,即可求出其顶点M的坐标,根据得出的A、B、M三点的坐标,即可用待定系数法求出抛物线的解析式.
(3)可先求出四边形ACMB的面积(由于四边形ACMB不规则,因此其面积可用分割法进行求解).然后根据ACMB的面求出P点的纵坐标的绝对值,将其代入抛物线的解析式中即可求出P点的坐标.
试题解析:(1)∵若x1,x2是方程x2﹣2(m﹣1)+m2﹣7=0的两个实数根,
由题意得:x1+x2═﹣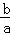 =2(m﹣1),x1x2=
=2(m﹣1),x1x2=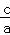 =m2﹣7.
=m2﹣7.
∴x12+x22=(x1+x2)2﹣2x1x2=4(m﹣1)2﹣2(m2﹣7)=10,
化简,得m2﹣4m+4=0,
解得m=2.
且当m=2时,△=4﹣4×(﹣3)>0,符合题意.
∴原方程可写成:x2﹣2x﹣3=0,
∵x1<x2,
∴x1=﹣1,x2=3;
∴A(﹣1,0),B(3,0);
(2)已知:A(﹣1,0),B(3,0),
∴抛物线的对称轴为x=1,
因此抛物线的顶点坐标为(1,﹣4).
设抛物线的解析式为y=a(x+1)(x﹣3),则有:
﹣4=a(1+1)(1﹣3),a=1;
∴y=(x﹣3)(x+1)=x2﹣2x﹣3;
当x=0时,y=-3.所以C(0,-3)
(3)S四边形ACMB=S△AOC+S梯形OCMN+S△NBM=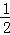 OA•OC+
OA•OC+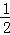 (OC+MN)•ON+
(OC+MN)•ON+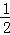 NB•MN,
NB•MN,
=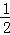 ×1×3+
×1×3+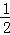 ×(3+4)×1+
×(3+4)×1+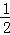 ×2×4=9.
×2×4=9.
假设存在P(x0,y0)使得S△PAB=2S四边形ACMB=18,
即: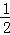 AB|y0|=18,
AB|y0|=18, ×4×|y0|=18,
×4×|y0|=18,
∴y0=±9;
当y0=9时,x2﹣2x﹣3=9,解得x=1﹣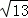 ,x=1+
,x=1+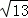 ;
;
当y0=﹣9时,x2﹣2x﹣3=﹣9,此方程无实数根.
∴存在符合条件的P点,且坐标为(1﹣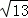 ,9),(1+
,9),(1+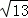 ,9).
,9).
考点:二次函数综合题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
 如图,如果∠CAE>∠BAD,那么下列说法中一定正确的是( )
如图,如果∠CAE>∠BAD,那么下列说法中一定正确的是( )| A、∠BAC>∠CAD | B、∠DAE>∠CAD | C、∠CAE<∠BAC+∠DAE | D、∠BAC<∠DAE |
查看答案和解析>>
科目:初中数学 来源:浙教版(新课标) 八年级下册 题型:
| |||||||
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜城市九年级上学期期中考试数学试卷(解析版) 题型:选择题
在等边三角形,矩形,平行四边形,菱形中,既是轴对称图形而又是中心对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知二次函数当x=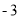 时,有最大值
时,有最大值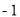 ,且当x=0时,y=
,且当x=0时,y= 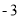 ,求二次函数的解析式。
,求二次函数的解析式。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜城市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分5分)已知关于 的一元二次方程方程
的一元二次方程方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求 的取值范围;
的取值范围;
(2)当 取最大整数时,不解方程直接写出方程的两根之和与两根之积.
取最大整数时,不解方程直接写出方程的两根之和与两根之积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级12月联考数学试卷(解析版) 题型:解答题
如图,⊙O的直径AB为10,弦BC为6,D、E分别为 ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由;
(3)直接写出CD的长为____________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市九年级上学期期中考试数学试卷(解析版) 题型:选择题
将抛物线 向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com