
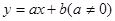 的图象与反比例函数
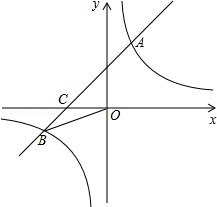
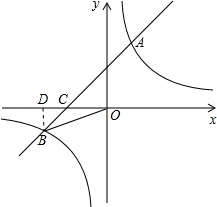
的图象与反比例函数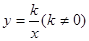 的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=
的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=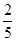 。
。
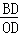 ,即
,即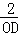 =
=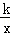 ,解得OD=5,
,解得OD=5,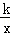 中,得k=xy=10,
中,得k=xy=10,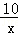 ,
,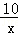 中,得m=5,∴A(2,5),
中,得m=5,∴A(2,5),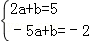 ,解得
,解得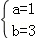 ,
,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 与一次函数y=-x+2的图象交于A、B两点,且点A的横坐标是-2.
与一次函数y=-x+2的图象交于A、B两点,且点A的横坐标是-2.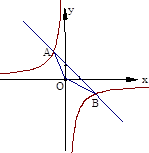
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点 在第二象限;
在第二象限; ,并写出点
,并写出点 的坐标;
的坐标; M的解析式y﹦kx+b进行探究:
M的解析式y﹦kx+b进行探究: 和点M的坐标.
和点M的坐标.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( )
(x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( )
| A.逐渐增大 | B.逐渐减小 | C.不变 | D.先增大后减小 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象上一点,过P点分别向x轴、y轴作垂线,所得的图中阴影部分的面积为6,则这个反比例函数的解析式为 ( )
的图象上一点,过P点分别向x轴、y轴作垂线,所得的图中阴影部分的面积为6,则这个反比例函数的解析式为 ( )
A. y=- | B.y= | C. y=- | D.y= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com