
【题目】某中学团委组织学生去儿童福利院慰问,准备购买15个甲种文具和20个乙种文具,共需885元;后翻阅商场海报发现,下周甲、乙两种文具进行促销活动,甲种文具打八折销售、乙种文具打九折,且打折后两种文具的销售单价相同.
(1)求甲、乙两种文具的原销售单价各为多少元?
(2)购买打折后的15个甲种文具和20个乙种文具,共可节省多少钱?
科目:初中数学 来源: 题型:
【题目】如右图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,有下列说法:①点
,有下列说法:①点![]() 与点
与点![]() 的距离是线段
的距离是线段![]() 的长;②点
的长;②点![]() 到直线
到直线![]() 的距离是线段
的距离是线段![]() 的长;③线段
的长;③线段![]() 是
是![]() 边
边![]() 上的高;④线段
上的高;④线段![]() 是
是![]() 边
边![]() 上的高.
上的高.
上述说法中,正确的个数为( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.

请将求![]() 的度数的过程及理由填写出来.
的度数的过程及理由填写出来.
解:∵![]() (已知),
(已知),
∴![]() (______________________).
(______________________).
又∵![]() (已知),
(已知),
∴![]() (______________________).
(______________________).
∴![]() __________(______________________).
__________(______________________).
∴![]() __________
__________![]() (______________________).
(______________________).
又∵![]() (已知),
(已知),
∴![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
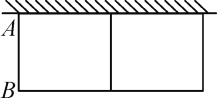
【题目】如图,为了美化街道,刘大爷准备利用自家墙外的空地种植两种不同的花卉,墙的最大可用长度是12.5m,墙外可用宽度为3.25m.现有长为21m的篱笆,计划靠着院墙围成一个中间有一道隔栏的长方形花圃.
(1)若要围成总面积为36m2的花圃,边AB的长应是多少?
(2)花圃的面积能否达到36.75m2?若能,求出边AB的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:在图1至图2中,已知![]() 的面积为a
的面积为a

(1)如图1,延长![]() 的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若
的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若![]() 的面积为
的面积为![]() ,则
,则![]() = (用含a的代数式表示);
= (用含a的代数式表示);
(2)在图1的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图2).若阴影部分的面积为
(如图2).若阴影部分的面积为![]() ,则
,则![]() = (用a含的代数式表示);
= (用a含的代数式表示);
(3)发现:像上面那样,将![]() 各边均顺次延长一倍,连接所得端点,得到
各边均顺次延长一倍,连接所得端点,得到![]() (如图2),此时,我们称
(如图2),此时,我们称![]() 向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是
向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是![]() 面积的 倍(用含n的代数式表示);
面积的 倍(用含n的代数式表示);
(4)应用:某市准备在市民广场一块足够大的空地上栽种牡丹花卉,工程人员进行了如下的图案设计:首先在![]() 的空地上种紫色牡丹,然后将
的空地上种紫色牡丹,然后将![]() 向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形
向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形![]() 的面积至多为多少平方米?
的面积至多为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD的各顶点坐标分别为A(1,0),B(2,0),C(2,2),D(0,1),四边形BFGH的各顶点坐标分别为F(4,0),G(4,4),H(0,2),则下列说法正确的是( )
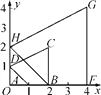
A. 四边形ABCD与四边形BFGH相似但不位似
B. 四边形ABCD与四边形BFGH位似但不相似
C. 四边形ABCD与四边形BFGH位似,且相似比为1∶![]()
D. 四边形ABCD与四边形BFGH位似,且相似比为1∶2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com