
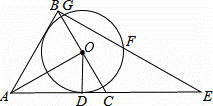
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
 (1)求证:AB与⊙O相切;
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长?
科目:初中数学 来源: 题型:
为响应国家的“一带一路”经济发展战略,树立品牌意识, 我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
我市质检部分对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
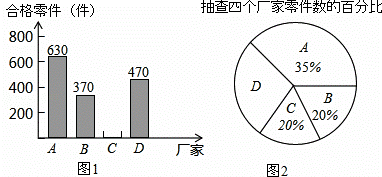
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ° ;
(2)抽查C厂家的合格率零件为 件,并将图1补充完整;
(3)通过计算说明合格率排在前两名的是哪两个厂家;
(4)若要从A、B、C、D四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用“列表法”或“画树形图”的方法求出(3)中两个厂家同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
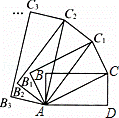
如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形ABnCnCn﹣1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
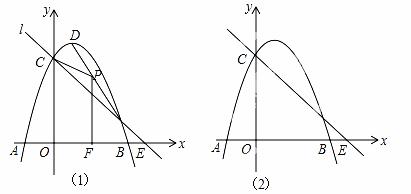
如图1,抛物线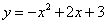 与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
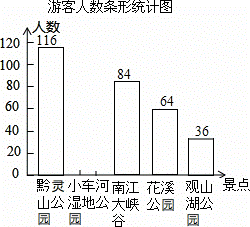
近年来,随着创建“生态文明城市”活动的开展,我市的社会知名度越来越高,吸引了很多外地游客,某旅行社对5月份本社接待外地游客来我市各景点旅游的人数作了一次抽样调查,并将调查结果绘制成如下两幅不完整的统计图表:
游客人数统计表
| 景点 | 频数(人数) | 频率 |
| 黔灵山公园 | 116 | 0.29 |
| 小车河湿地公园 | 0.25 | |
| 南江大峡谷 | 84 | 0.21 |
| 花溪公园 | 64 | 0.16 |
| 观山湖公园 | 36 | 0.09 |
(1)此次共调查 人,并补全条形统计图;
(2)由上表提供的数据可以制成扇形统计图,求“南江大峡谷”所对的圆心角的度数;
(3)该旅行社预计7月份接待来我市的游客有2500人,根据以上信息,请你估计去黔灵山公园的游客大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com