
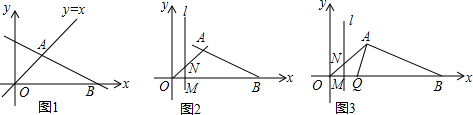
���� ��1������A���������y=x�������a=3��Ȼ�����ô���ϵ���������ֱ��AB�Ľ���ʽ��
��2���ٵ�����N��OA��ʱ����y=2����y=x������õ�N������Ϊ��2��2�����Ӷ��ɵõ�ֱ��l�Ľ���ʽΪx=2��Ȼ����Գ�ͼ�ε����ʿ���õ�Q�����꣬������N��AB��ʱ����y=2����ֱ��AB�Ľ���ʽ����N������Ϊ��2��2�����Ӷ��ɵõ�ֱ��l�Ľ���ʽΪx=2��Ȼ����Գ�ͼ�ε����ʿ���õ�Q�����ꣻ
�������AB�ij���Ȼ����ݡ�AQB=90����QAB=90����з�����㼴�ɣ�
��� �⣺��1���߽���3��a������y=x�ã�a=3��
���A��������3��3����
��ֱ��AB�Ľ���ʽΪy=kb+b������A��B���������ã�$\left\{\begin{array}{l}{3k+b=3}\\{9k+b=0}\end{array}\right.$��
��ã�$k=-\frac{1}{2}$��b=$\frac{9}{2}$��
��ֱ��AB�Ľ���ʽΪy=$-\frac{1}{2}x+\frac{9}{2}$��
��2���ٵ���N��OA��ʱ��
�߽�y=2����y=x�ã�x=2��
���N��������2��2����
��ֱ��l�Ľ���ʽΪx=2��
�ߵ�Q���O����l�Գƣ�
���Q��������4��0����
����N��AB��ʱ��
�߽�y=2����y=-$\frac{1}{2}x+\frac{9}{2}$��x=5��
���N��������5��2����
��ֱ��l�Ľ���ʽΪx=5��
�ߵ�Q���O����x=5�Գƣ�
���Q��������10��0����
�ڡߵ�A��3��3����B��9��0����
��AB=$\sqrt{��9-3��^{2}+��3-0��^{2}}$=3$\sqrt{5}$��
����QAB=90��ʱ��
��ֱ��AB��һ����ϵ��k=-$\frac{1}{2}$��
��QB=AB��$\frac{\sqrt{5}}{2}$=3$\sqrt{5}$��$\frac{\sqrt{5}}{2}$=7.5��
��OQ=1.5��
���N�ĺ�����Ϊ$\frac{3}{4}$��
��x=$\frac{3}{4}$ʱ������y=x�ã�y=$\frac{3}{4}$��
��MN=$\frac{3}{4}$��
����AQB=90ʱ��AQ��OB��
���Q�ĺ�����Ϊ3��
���M�ĺ�����Ϊ1.5��
��x=1.5����y=x�ã�y=1.5��
��MN=1.5��
�ʴ�Ϊ��1.5��$\frac{3}{4}$��
���� ������Ҫ�������һ�κ������ۺ�Ӧ�á�����ϵ������һ�κ����Ľ���ʽ����Գ�ͼ�ε����ʣ����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
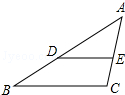 ��ͼ���ڡ�ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ���DE��BC��AD=4��BD=2����$\frac{DE}{BC}$��ֵ��
��ͼ���ڡ�ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ���DE��BC��AD=4��BD=2����$\frac{DE}{BC}$��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
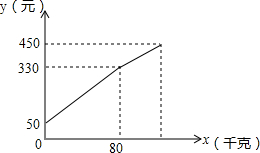 ���ү��ÿǧ��2.1Ԫ������һ���Ϸ����ٵ����ϳ��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����Ȱ��г��۳�һЩ���ֽ��ͳ��ۣ��۳�����ǧ����x�������г��е�Ǯ��yԪ����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺
���ү��ÿǧ��2.1Ԫ������һ���Ϸ����ٵ����ϳ��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����Ȱ��г��۳�һЩ���ֽ��ͳ��ۣ��۳�����ǧ����x�������г��е�Ǯ��yԪ����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com