
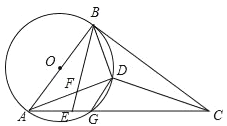
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
【答案】(1)证明见解析;(2)证明见解析;(3)正确的结论:AD﹣BD的值不变,证明见解析,AD﹣BD=![]() .
.
【解析】试题分析:(1)根据三角形内心的性质得出∠DBC=∠DBE,进而根据已知求得∠DBC=∠BAD,根据圆周角定理即可证得![]() 从而求得AB⊥BC,证得结论;
从而求得AB⊥BC,证得结论;
(2)连接![]() ,根据圆内接四边形外角的性质得出
,根据圆内接四边形外角的性质得出![]() 由三角形外角的性质求得
由三角形外角的性质求得![]() 证得
证得![]() 进而求得
进而求得![]() 由三角形内心的性质得出
由三角形内心的性质得出![]() 然后根据AAS证得△DEF≌△DEG,从而证得
然后根据AAS证得△DEF≌△DEG,从而证得![]()
(3)在AD上截取DH=BD,连接BH、BG,证得![]() 是等腰直角三角形,得出
是等腰直角三角形,得出![]() 然后证得△ABH∽△GBD,得出
然后证得△ABH∽△GBD,得出![]() 求得
求得![]() 即可求得
即可求得![]()
试题解析:(1)证明:∵D为△BCE内心,
∴∠DBC=∠DBE,
∵∠DBE=∠BAD.
∴∠DBC=∠BAD,
∵AB是![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
即![]()
∴AB⊥BC,
∴BC是![]() 的切线;
的切线;
(2)证明:如图1,连接DE,

∵∠DBC=∠BAD,∠DBC=∠DBE,
∴∠DBE=∠BAD,
∴∠ABF+∠BAD=∠ABF+∠DBE,
∴∠BFD=∠ABD,
∵∠DGC=∠ABD,
∴∠BFD=∠DGC,
∴∠DFE=∠DGE,
∵D为△BCE内心,
∴∠DEG=∠DEB,
在△DEF和△DEG中
 ,
,
∴△DEF≌△DEG(AAS),
∴DF=DG;
(3)ADBD的值不变;

如图2,在AD上截取DH=BD,连接BH、BG,
∵AB是直径,
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴∠AHB=∠BDG,
∵∠BAD=∠BGD,
∴△ABH∽△GBD,
∴![]()
∵DG=1,
∴![]()
∵ADBD=ADDH=AH,
∴![]()


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
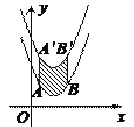
【题目】如图,将二次函数y=![]() (x-2)2+1的图像沿y轴向上平移得到一条新的二次函数图像,其中A(1,m),B(4,n)平移后对应点分别是A′、B′,若曲线AB所扫过的面积为12(图中阴影部分),则新的二次函数对应的函数表达是__________________.
(x-2)2+1的图像沿y轴向上平移得到一条新的二次函数图像,其中A(1,m),B(4,n)平移后对应点分别是A′、B′,若曲线AB所扫过的面积为12(图中阴影部分),则新的二次函数对应的函数表达是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
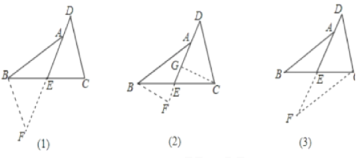
【题目】读下面的题目及分析过程,并按要求进行证明。已知:如图,E是BC的中点,点A在DB上,且
∠BAE=∠CDE,求证:AB=CD
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等。因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形。现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明。
图(1):延长DE到F使得EF=DE
图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F
图(3):过C点作CF∥AB交DE的延长线于F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行调查,根据调查结果绘制成如下两幅不完整的统计图.
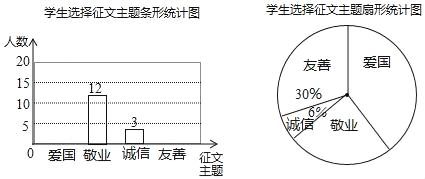
(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,“爱国”主题所对应的圆心角是多少;
(4)如果该校七年级共有![]() 名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(![]() ,0)、(0,4),抛物线
,0)、(0,4),抛物线![]() 经过B点,且顶点在直线
经过B点,且顶点在直线![]() 上.
上.

【1】(1)求抛物线对应的函数关系式;
【2】(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
【3】(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
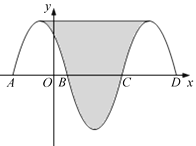
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com