
【题目】已知抛物线![]() 与
与![]() 形状相同,开口方向不同,其中抛物线
形状相同,开口方向不同,其中抛物线![]() :
:![]() 交x轴于A,B两点
交x轴于A,B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,且
,且![]() ,抛物线
,抛物线![]() 与
与![]() 交于点A与
交于点A与![]() .
.
![]() 求抛物线
求抛物线![]() ,
,![]() 的函数表达式;
的函数表达式;
![]() 当x的取值范围是______时,抛物线
当x的取值范围是______时,抛物线![]() 与
与![]() 上的点的纵坐标同时随横坐标的增大而增大;
上的点的纵坐标同时随横坐标的增大而增大;
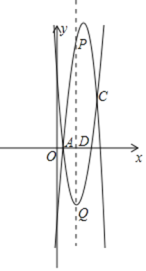
![]() 直线
直线![]() 轴,分别交x轴,
轴,分别交x轴,![]() ,
,![]() 于点
于点![]() ,P,Q,当
,P,Q,当![]() 时,求线段PQ的最大值.
时,求线段PQ的最大值.
【答案】![]() 的函数表达式为
的函数表达式为![]() ,
,![]() 的函数表达式为
的函数表达式为![]() ;
;![]() ;
;![]() 16.
16.
【解析】
![]() 利用二次函数图象上点的坐标特征可得出点A,B的横坐标,由
利用二次函数图象上点的坐标特征可得出点A,B的横坐标,由![]() 可得出关于a的方程,解之即可得出a的值,进而可得出抛物线
可得出关于a的方程,解之即可得出a的值,进而可得出抛物线![]() 的函数表达式,利用二次函数图象上点的坐标特征可得出点A,C的坐标,由点A,C的坐标,利用待定系数法即可求出抛物线
的函数表达式,利用二次函数图象上点的坐标特征可得出点A,C的坐标,由点A,C的坐标,利用待定系数法即可求出抛物线![]() 的函数表达式;
的函数表达式;
![]() 利用二次函数的性质分别找出抛物线
利用二次函数的性质分别找出抛物线![]() ,
,![]() 上点的纵坐标随横坐标的增大而增大的x的取值范围,取其公共部分即可得出结论;
上点的纵坐标随横坐标的增大而增大的x的取值范围,取其公共部分即可得出结论;
![]() 利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可得出PQ的长度,分
利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可得出PQ的长度,分![]() ,
,![]() 及
及![]() 三种情况找出PQ的最大值,取其中的最大值即可得出结论.
三种情况找出PQ的最大值,取其中的最大值即可得出结论.
解:![]() 当
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() .
.![]() ,
,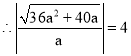 ,
,![]() ,
,![]() 抛物线
抛物线![]() 的函数表达式为
的函数表达式为![]() .
.
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() .
.
当![]() 时,
时,![]() ,
,![]() 点C的坐标为
点C的坐标为![]() .
.
设抛物线![]() 的函数表达式为
的函数表达式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,得:
,得:![]() ,
,
解得:![]() ,
,![]() 抛物线
抛物线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 当
当![]() 时,抛物线
时,抛物线![]() 上的点的纵坐标随横坐标的增大而增大,
上的点的纵坐标随横坐标的增大而增大,
当![]() 时,抛物线
时,抛物线![]() 上的点的纵坐标随横坐标的增大而增大.
上的点的纵坐标随横坐标的增大而增大.![]() 当
当![]() 时,抛物线
时,抛物线![]() 与
与![]() 上的点的纵坐标同时随横坐标的增大而增大.
上的点的纵坐标同时随横坐标的增大而增大.
故答案为:![]() .
.![]() 点P的坐标为
点P的坐标为![]() ,
,![]() 点P的坐标为
点P的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,
,![]() .
.![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() 随着n的增大而减小,
随着n的增大而减小,![]() 当
当![]() 时,PQ取得最大值,最大值为7;
时,PQ取得最大值,最大值为7;![]() 时,
时,![]() ,
,![]() ,
,![]() 当
当![]() 时,PQ取得最大值,最大值为9;
时,PQ取得最大值,最大值为9;![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() 随着n的增大而增大,
随着n的增大而增大,![]() 当
当![]() 时,PQ取得最大值,最大值为16.
时,PQ取得最大值,最大值为16.
综上所述:当![]() 时,线段PQ的最大值为16.
时,线段PQ的最大值为16.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
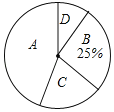
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)

(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
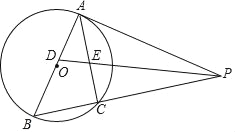
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年国庆期间解放碑、洪崖洞、朝天门、来福士、长嘉汇等景点人员密集;穿楼而过的轻轨、洪崖洞、灯光秀……吸引着海量游客前来重庆打卡.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在中秋节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2000名,鸳鸯火锅和红汤火锅的人均消费分别为180元和120元.
(1)中秋节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“国庆”节期间,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与中秋节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了![]() a%,最终“国庆”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
a%,最终“国庆”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
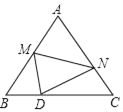
【题目】如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为w元,当每间房价定价为多少元时,宾馆每天所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com