Question

【题目】如图，以AB为直径的⊙O外接于△ABC，过A点的切线AP与BC的延长线交于点P，∠APB的平分线分别交AB，AC于点D，E，其中AE，BD（AE＜BD）的长是一元二次方程x2﹣5x+6=0的两个实数根．

（1）求证：PABD=PBAE；

（2）在线段BC上是否存在一点M，使得四边形ADME是菱形？若存在，请给予证明，并求其面积；若不存在，说明理由．

Answer 1

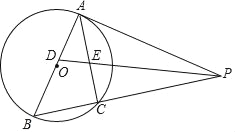
【答案】（1）证明见解析；（2）存在，

【解析】（1）易证∠APE=∠BPD，∠EAP=∠B，从而可知△PAE∽△PBD，利用相似三角形的性质即可求出答案．

（2）过点D作DF⊥PB于点F，作DG⊥AC于点G，易求得AE=2，BD=3，由（1）可知：，从而可知cos∠BDF=cos∠BAC=cos∠APC=，从而可求出AD和DG的长度，进而证明四边形ADFE是菱形，此时F点即为M点，利用平行四边形的面积即可求出菱形ADFE的面积．

（1）∵PD平分∠APB，

∴∠APE=∠BPD，

∵AP与⊙O相切，

∴∠BAP=∠BAC+∠EAP=90°，

∵AB是⊙O的直径，

∴∠ACB=∠BAC+∠B=90°，

∴∠EAP=∠B，

∴△PAE∽△PBD，

∴，

∴PABD=PBAE；

（2）如图，过点D作DF⊥PB于点F，作DG⊥AC于点G，

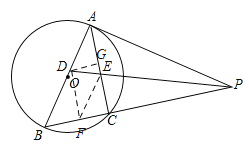
∵PD平分∠APB，AD⊥AP，DF⊥PB，

∴AD=DF，

∵∠EAP=∠B，

∴∠APC=∠BAC，

易证：DF∥AC，

∴∠BDF=∠BAC，

由于AE，BD（AE＜BD）的长是x2﹣5x+6=0的两个实数根，

解得：AE=2，BD=3，

∴由（1）可知：，

∴cos∠APC=，

∴cos∠BDF=cos∠APC=，

∴，

∴DF=2，

∴DF=AE，

∴四边形ADFE是平行四边形，

∵AD=DF，

∴四边形ADFE是菱形，此时点F即为M点，

∵cos∠BAC=cos∠APC=，

∴sin∠BAC=，

∴，

∴DG=，

∴菱形ADME的面积为：DGAE=2×=.