
【题目】爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题.
例如:![]()
![]() ;因此
;因此![]() 有最小值是1,只有当
有最小值是1,只有当![]() 时,才能得到这个式子的最小值1.
时,才能得到这个式子的最小值1.
同样![]() ,因此
,因此![]() 有最大值是8,只有当
有最大值是8,只有当![]() 时,才能得到这个式子的最大值8.
时,才能得到这个式子的最大值8.
(1)当x= 时,代数式﹣2(x﹣3)2+5有最大值为 .
(2)当x= 时,代数式2x2+4x+3有最小值为 .
(3)矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的小门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少?
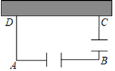
【答案】(1)3,5;(2)-1,1;(3)32.
【解析】
(1)类比例子得出答案即可;
(2)根据题意利用配方法配成(1)中的类型,进一步确定最值即可;
(3)根据题意利用长方形的面积列出式子,利用(1)(2)的方法解决问题.
解:(1)在代数式-2(x-3)2+5中,当x=3时,有最大值5,
故答案为:3、5;
(2)∵2x2+4x+3=2(x2+2x+1-1)+3=2(x+1)2+1,
∴当x=-1时,代数式2x2+4x+3有最小值为1,
故答案为:-1、1;
(3)设AD=x,则AB=14-(x+x-1)+1=16-2x,
∵S=x(16-2x)=-2(x-4)2+32,
∴当AD=4m时,面积最大值为32m2.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)B点的对应点B′的坐标是 ;C点的对应点C′的坐标是 ;
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上,若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
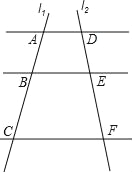
【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
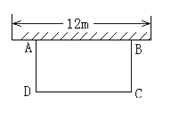
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为![]() m,DC的长为
m,DC的长为![]() m。
m。
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量![]() 能否取值为4m,若能,求出
能否取值为4m,若能,求出![]() 的值,若不能,请说明理由;
的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
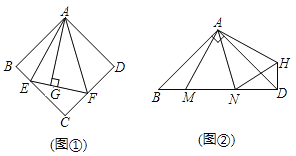
【题目】![]() 如图
如图![]() ,在正方形ABCD中,
,在正方形ABCD中,![]() 的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求
的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求![]() 的度数.
的度数.
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且![]() ,将
,将![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 至
至![]() 位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
![]() 在图
在图![]() 中,连接BD分别交AE,AF于点M,N,若
中,连接BD分别交AE,AF于点M,N,若![]() ,
,![]() ,
,![]() ,求AG,MN的长.
,求AG,MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDGF周长的最小值为![]() ,其中,判断正确的序号是( )
,其中,判断正确的序号是( )
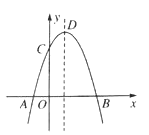
A.①②B.②③C.①③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成.
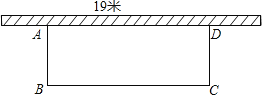
(1)若围成的面积为180m,试求出自行车车棚的长和宽;
(2)能围成的面积为200m自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com